In the previous article, you learned about inverse of matrix and why it is important. You will learn how to find inverse of a matrix in this article. There are two primary method of finding inverse of any square invertible matrix – Classical adjoint method and Gauss -Jordan elimination method.
Methods To Find Inverse Of Matrix
The primary method of finding of inverse of matrix are
- Classical adjoint method
- Gauss-Jordan elimination method
Throughout this article, we will discuss about these two methods in detail.
Classical Adjoint Method
If ![]() is an invertible matrix then we can find the inverse of matrix
is an invertible matrix then we can find the inverse of matrix ![]() with the adjoint of matrix
with the adjoint of matrix ![]() .
.
But,before we begin you must understand a few terminologies.
Determinant – It is a special number obtained from a square matrix, non-square matrix do not have determinants. If ![]() is a square matrix then there is a number of ways to denote its determinant.
is a square matrix then there is a number of ways to denote its determinant.
\begin{aligned}
&A = \begin{bmatrix}a & b\\c & d\end{bmatrix}\\\\
&det(A) \hspace{5px} or \hspace{5px}\begin{vmatrix}A\end{vmatrix} \hspace{5px} or \hspace{5px}\begin{vmatrix}a & b\\c & d\end{vmatrix}\\\\
&det(A)= ad - bc
\end{aligned}Minor of a matrix – The minor of a square matrix is determinant obtained by deleting a row and a column from the determinant of a larger square matrix. It is denoted by ![]() for element
for element ![]() where
where ![]() is the ithrow and
is the ithrow and ![]() is the jth column.
is the jth column.
The determinant of 2 x 2 matrix.
\begin{aligned}
&det(A) =\begin{vmatrix}a & b\\c & d\end{vmatrix}\\\\
&M_{11} = \begin{vmatrix}a & b\\c & d\end{vmatrix} = \begin{vmatrix}d\end{vmatrix}= d\\\\
&M_{12} = \begin{vmatrix}a & b\\c & d\end{vmatrix} = \begin{vmatrix}c\end{vmatrix}= c\\\\
&M_{21} = \begin{vmatrix}a & b\\c & d\end{vmatrix} = \begin{vmatrix}b\end{vmatrix}= b\\\\
&M_{22} = \begin{vmatrix}a & b\\c & d\end{vmatrix} = \begin{vmatrix}a\end{vmatrix}= a\\\\
\end{aligned}You get following matrix of determinant.
= \begin{bmatrix}d & c\\b & a\end{bmatrix}Cofactor of a Matrix – The cofactor of a matrix can be found from determinant of minors by assigning appropriate negative or positive signs. Each cofactor ![]() can be found by following equation.
can be found by following equation.
\begin{aligned}
&A_{ij}= (-1)^{i+j}M_{ij}\\\\
&A_{11}= (-1)^2 \times det(d) = d\\\\
&A_{12}= (-1)^3 \times det(c) = -c\\\\
&A_{21}= (-1)^3 \times det(b) = -b\\\\
&A_{22}= (-1)^4 \times det(a) = a
\end{aligned}Adjoint of a Matrix – The adjoint of a matrix is obtained by transposing the co-factor matrix. It is denoted as ![]() .
.
\begin{aligned}
adj A = \left(A_{ij}\right)^T = \begin{bmatrix}d & -b\\-c & a\end{bmatrix}
\end{aligned}Finding Inverse Of Matrix Through Adjoint Method
The process of finding inverse of matrix using adjoint method is as follows.
- Find the matrix of minors
- Find the matrix of co-factors
- Find the determinant det(A) by multiplying first row of matrix A with first row of co-factor matrix of A.
- Find the adjoint matrix usign co-factor matrix of A.
- Multiply 1/det(A) with adjoint of A (adj A) to get the inverse matrix of A.
We will find inverse of a matrix using the adjoint of matrix in the next section. First we must find the inverse of ![]() matrix, then
matrix, then ![]() and finally
and finally ![]() matrix.
matrix.
Example #1 : Find the inverse of ![]() matrix using adjoint method.
matrix using adjoint method.
A = \begin{bmatrix}3\end{bmatrix}Solution:
![]()
Step 1: There is no minor for 1×1 matrix.
Step 2: There is no cofactor for 1×1 matrix.
Step 3: The determinant of A is ![]() .(invertible)
.(invertible)
Step 4: The adjoint of matrix A is ![]() .
.
To compute the inverse of matrix A use
\begin{aligned}
&A^{-1} = 1/det(A) \times \begin{bmatrix}1\end{bmatrix}\\\\
&A^{-1} = 1/3 \times \begin{bmatrix}1\end{bmatrix}\\\\
&A^{-1} = 1/3
\end{aligned}Example #2 : Find the inverse of ![]() matrix using adjoint method.
matrix using adjoint method.
B = \begin{bmatrix}2 & 1\\3 & 7\end{bmatrix}Solution:
Let ![]() be a square and invertible matrix of order
be a square and invertible matrix of order ![]() .
.
Step 1: The minors of matrix ![]() are
are
\begin{aligned}
&M_{11} = \begin{vmatrix}7\end{vmatrix}= 7\\\\
&M_{12} = \begin{vmatrix}3\end{vmatrix}= 3\\\\
&M_{21} = \begin{vmatrix}1\end{vmatrix}= 1\\\\
&M_{22} = \begin{vmatrix}2\end{vmatrix}= 2
\end{aligned}The minor matrix is,
Step 2: The cofactor of matrix ![]() is obtained from minor matrix.
is obtained from minor matrix.
\begin{aligned}
&B_{11} = (-1)^{1+1}M_{11} = 7\\\\
&B_{12} = (-1)^{1+2}M_{12} = -3\\\\
&B_{21} = (-1)^{2+1}M_{21} = -1\\\\
&B_{22} = (-1)^{2+2}M_{22} = 2
\end{aligned}The cofactor matrix is,
= \begin{bmatrix}7 & -3\\-1 & 2\end{bmatrix}Step 3: To compute the determinant simply multiply corresponding elements of top row of matrix ![]() and tow row of cofactor of
and tow row of cofactor of ![]() and add them.
and add them.
Top row of matrix B = 2, 1
Top row of cofactor matrix = 7 -3
det(B) = 2 \times 7 + 1 \times (-3) = 14 - 3 = 11
Step 4: Find the adjoint of the matrix ![]() by transposing cofactor matrix.
by transposing cofactor matrix.
\begin{aligned}
&cofactor \hspace{1ex} of \hspace{1ex} B = \begin{bmatrix}7 & -3\\-1 & 2\end{bmatrix}\\\\
&adj B = \begin{bmatrix}B_{ij}\end{bmatrix}^T\\\\
&adj B = \begin{bmatrix}7 & -1\\-3 & 2\end{bmatrix}
\end{aligned}To find the inverse of matrix ![]() use following.
use following.
\begin{aligned}
&B^{-1} = 1/11 \times \begin{bmatrix}7 & -1\\-3 & 2\end{bmatrix}\\\\
&B^{-1} = \begin{bmatrix}7/11 & -1/11\\-3/11& 2/11\end{bmatrix}
\end{aligned}Verify the inverse of matrix ![]() .
.
\begin{aligned}
&BB^{-1} = B^{-1}B = I\\\\
&= \begin{bmatrix}2 & 1\\3 & 7\end{bmatrix} \times \begin{bmatrix}7/11 & -1/11\\-3/11& 2/11\end{bmatrix}\\\\
&= \begin{bmatrix}14/11 + -3/11& -2/11+ 2/11\\21/11 + -21/11& -3/11+ 14/11\end{bmatrix}\\\\
&= \begin{bmatrix}11/11&0\\0&11/11\end{bmatrix}\\\\
&= \begin{bmatrix}1&0\\0&1\end{bmatrix}
\end{aligned}Example #3 : Find the inverse of 3 x 3 matrix using the adjoint method.
A = \begin{bmatrix}1 & -2 & 1\\6 & 2 & 3\\2 & 1 & 4\end{bmatrix}Solution :
Given the matrix ![]() of order
of order ![]() .
.
A = \begin{bmatrix}1 & -2 & 1\\6 & 2 & 3\\2 & 1 & 4\end{bmatrix}Step 1: Find the minors of the matrix ![]() .
.
\begin{aligned}
&M_{11} = \begin{vmatrix}a_{22}.a_{33}-a_{23}.a_{32}\end{vmatrix} = \begin{vmatrix}8 - 3\end{vmatrix} = 5\\\\
&M_{12} = \begin{vmatrix}a_{21}.a_{33}-a_{23}.a_{31}\end{vmatrix} = \begin{vmatrix}24 - 6 \end{vmatrix}= 18\\\\
&M_{13} = \begin{vmatrix}a_{21}.a_{32}-a_{22}.a_{31}\end{vmatrix} = \begin{vmatrix}6 - 4\end{vmatrix} = 2\\\\
&M_{21} = \begin{vmatrix}a_{12}.a_{33}-a_{13}.a_{32}\end{vmatrix} = \begin{vmatrix}-8 - 1\end{vmatrix} = -9\\\\
&M_{22} = \begin{vmatrix}a_{11}.a_{33}-a_{13}.a_{31}\end{vmatrix} = \begin{vmatrix}4 - 2\end{vmatrix} = 2\\\\
&M_{23} = \begin{vmatrix}a_{11}.a_{32}-a_{12}.a_{31}\end{vmatrix} = \begin{vmatrix}1 + 4 \end{vmatrix}= 5\\\\
&M_{31} = \begin{vmatrix}a_{12}.a_{23}-a_{13}.a_{22}\end{vmatrix} = \begin{vmatrix}-6 - 2\end{vmatrix} = -8\\\\
&M_{32} = \begin{vmatrix}a_{11}.a_{23}-a_{13}.a_{21}\end{vmatrix} = \begin{vmatrix}3 - 6\end{vmatrix} = -3\\\\
&M_{33} = \begin{vmatrix}a_{11}.a_{22}-a_{12}.a_{21}\end{vmatrix} = \begin{vmatrix}2 + 12\end{vmatrix} = 14
\end{aligned}We have the following matrix of minors.
\begin{bmatrix}5 & 18 & 2\\-9 & 2 & 5\\-8 & -3 & 14\end{bmatrix}Step 2: Find the cofactors of matrix ![]() .
.
We can use the matrix of minors to find the matrix of cofactors.
\begin{aligned}
&A_{11} = (-1)^2 . 5 = 5\\
&A_{12} = (-1)^3 . 18 = -18\\
&A_{13} = (-1)^4 . 2 = 2\\\\
&A_{21} = (-1)^3 . -9 = 9\\
&A_{22} = (-1)^4 . 2 = 2\\
&A_{23} = (-1)^5 . 5 = -5\\\\
&A_{31} = (-1)^4 . -8 = -8\\
&A_{32} = (-1)^5 . -3 = 3\\
&A_{33} = (-1)^4 . 14 = 14
\end{aligned} We get the cofactor matrix of ![]() .
.
= \begin{bmatrix}5 & -18 & 2\\9 & 2 & -5\\-8 & 3 & 14\end{bmatrix}Step 3: Find determinant of the matrix ![]() .
.
Top row of matrix A = 1, -2, 1
Top row of coactor of A = 5, -18, 2
det(A) = (1)(5)+ (-2)(-18) + (1)(2) = 5 + 36 + 2 = 43
Step 4: Find the adjoint of matrix ![]() . The adjoint of the matrix can be obtained from transposing the cofactor matrix.
. The adjoint of the matrix can be obtained from transposing the cofactor matrix.
\begin{aligned}
&Adj A = \begin{bmatrix}A_{ij}\end{bmatrix}^T = \begin{bmatrix} 5 & -18 & 2\\9 & 2 & -5\\-8 & 3 & 14\end{bmatrix}^T\\\\
&Adj A = \begin{bmatrix} 5 & 9 & -8\\-18& 2 & 3\\2 & -5 & 14\end{bmatrix}
\end{aligned}Step 5: Find the inverse of matrix ![]() using following equation.
using following equation.
\begin{aligned}
&A^{-1} = 1/det(A) \times Adj A\\\\
&A^{-1} = 1/43 \times \begin{bmatrix} 5 & 9 & -8\\-18& 2 & 3\\2 & -5 & 14\end{bmatrix}\\\\
&A^{-1} = \begin{bmatrix}5/43& 9/43& -8/ 43\\-18/43& 2/43& 3/43\\2/43& -5/43&14/43\end{bmatrix}
\end{aligned}Verify that ![]() .
.
Verify results:
\begin{aligned}
&= \begin{bmatrix}1 & -2 & 1\\6 & 2 & 3\\2 & 1 & 4\end{bmatrix} \times \begin{bmatrix}5/43&9/ 43& -8/ 43\\-18/43& 2/43& 3/43\\2/43& -5/43&14/43\end{bmatrix}\\\\
& = \begin{bmatrix}5/43+ 36/43+2/43& 9/43 +( -4)/43 + (-5)/43& -8/43+ 6/43+14/43\\30/43+( -36)/43+ 6/43& 54/43+4/43+ (-15)/43& -48/43+6/43+42/43\\10/43+(-18)/43+ 8/43&18/43+2/43+ (-20)/43& -16/43+3/43+56/43\end{bmatrix}\\\\
& =\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\1 & 0 & 0\end{bmatrix}
\end{aligned}Finding Inverse of Matrix Using Gauss-Jordan Elimination Method
The Gauss-Jordan elimination method convert a matrix into reduced-row echelon form to find the value of solution vector ![]() in
in ![]() , but here we use the technique to find inverse matrix
, but here we use the technique to find inverse matrix ![]() .
.
Row Operations
The Gauss-Jordan technique involves row operations on augmented matrix ![]() obtained from the system of linear equations that transforms the matrix into identity matrix
obtained from the system of linear equations that transforms the matrix into identity matrix ![]() where
where ![]() is the order of matrix
is the order of matrix ![]() .
.
These row operations are
- Multiply a row
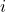 with scalar
with scalar  where
where 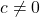 .
. - Interchange row
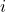 with row
with row 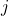 .
. - Addition of
 times row
times row 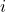 to row
to row 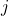 .
.
Example #5 : Row operations
Let ![]() be matrix of order
be matrix of order ![]() .
.
A = \begin{bmatrix}1 & 3\\2 & 1\end{bmatrix}Multiply a row 1 with 3.
R_1 \times 3 = \begin{bmatrix}3 & 9\\2 & 1\end{bmatrix}Interchange row 2 with row 1.
R_2 \Leftrightarrow R_1 = \begin{bmatrix}2 & 1\\3 & 9\end{bmatrix}Add 2 times row 1 to row 2.
2R_1 + R_2 = \begin{bmatrix}2 & 1\\7 & 11\end{bmatrix}Elementary Matrix
An elementary matrix ![]() is a matrix obtained from performing a single row operation on identity matrix
is a matrix obtained from performing a single row operation on identity matrix ![]() .
.
Suppose A is a matrix of order ![]() , then the product
, then the product ![]() is same as performing that row operation on matrix
is same as performing that row operation on matrix ![]() .
.
Example #6 : Elementary Matrix
Suppose ![]() is a matrix of order
is a matrix of order ![]() .
.
A = \begin{bmatrix}1 & 5 & 8\\2 & 1 & 3\\0 & 1 & 6\end{bmatrix}Let ![]() be row operation
be row operation ![]() on
on ![]() of order
of order ![]() .
.
Let \hspace{5px} E = \begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\2 & 0 & 1\end{bmatrix}Let us perform ![]() on
on ![]() .
.
= \begin{bmatrix}1 & 5 & 8\\2 & 1 & 3\\2 & 11 & 22\end{bmatrix} \hspace{5px} (1)Now, let us find ![]() matrix.
matrix.
\begin{aligned}
&EA = \begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\2 & 0 & 1\end{bmatrix} \times \begin{bmatrix}1 & 5 & 8\\2 & 1 & 3\\0 & 1 & 6\end{bmatrix}\\\\
&EA = \begin{bmatrix}1+0+0 & 5+0+0 & 8+0+0\\0+2+0 & 0+1+0 & 0+3+0\\2+0+0 & 10+0+1 & 16+0+6\end{bmatrix}\\\\
&EA = \begin{bmatrix}1 & 5 & 8\\2 & 1 & 3\\2 & 11 & 22\end{bmatrix}\hspace{5px} (2)
\end{aligned}Therefore, (1) and (2) are same.
Inverse Operations
If matrix ![]() is a result of row operation on identity matrix
is a result of row operation on identity matrix ![]() , then there exists some operation if performed on
, then there exists some operation if performed on ![]() will give back
will give back ![]() . Such an operation is called an Inverse operation.
. Such an operation is called an Inverse operation.
For every elementary row operation, there is an equivalent inverse operation. Check the table below.
| Elementary Row Operation | Inverse Operation |
| Multiply row i by c where c != 0 | Multiply row i by 1/c |
| Interchange row i with row j | Interchange row j with row i |
| Add k times row i to row j | Add -k times row i to row j |
Example #7 : Inverse Operations
Multiply row ![]() by
by ![]() .
.
\begin{aligned}
&E = k \times R_1 = 3 \times \begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}\\\\
&E = \begin{bmatrix}3 & 0\\0 & 1\end{bmatrix}
\end{aligned}Multiply row ![]() by
by ![]() where
where ![]()
\begin{aligned}
&1/3 \times R_1 = 1/3\times \begin{bmatrix}3 & 0\\0 & 1\end{bmatrix}\\\\
&I = \begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}
\end{aligned}From the above we can conclude that
1. Some operation on ![]() give the elementary matrix
give the elementary matrix ![]() .
.
2. The inverse of previous operation on E will give back ![]() .
.
3. Inverse operation on ![]() will result in an inverse matrix
will result in an inverse matrix ![]() such that
such that
E.E^{-1} = E^{-1}.E = INote that ![]() is invertible matrix and has determinant greater than 0.
is invertible matrix and has determinant greater than 0.
4 Necessary Statements For Gauss-Jordan technique and inverses
Before we find inverse of a matrix ![]() using Gauss-Jordan technique, there are 4 necessary prepositions that must be true about the matrix
using Gauss-Jordan technique, there are 4 necessary prepositions that must be true about the matrix ![]() and its inverse.
and its inverse.
If matrix ![]() is
is ![]() square matrix these 4 statement must always be true.
square matrix these 4 statement must always be true.
- Matrix
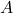 is invertible meaning the determinant is greater than 0 and does not have a zero row.
is invertible meaning the determinant is greater than 0 and does not have a zero row. 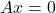 has only trivial solution.
has only trivial solution.- The matrix
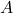 is reduced to reduced-row echelon form which is identity matrix
is reduced to reduced-row echelon form which is identity matrix 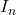 . This is because
. This is because 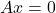 has trivial solution only, which means
has trivial solution only, which means 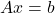 has one solution for every
has one solution for every 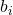 .
.
\begin{bmatrix}x_1& 0& 0& 0 & b_1\\0& x_2&0 & 0& b_2\\0 & 0& x_3 & 0 & b_3\\0& 0& 0 & x_n & b_n\end{bmatrix}- The matrix
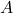 is product of elementary matrices.
is product of elementary matrices.
Multiplying A with elementary matrices is same as performing row operations on A which will reduce the matrix to identity matrix ![]() .
.
E_1E_2 ... E_n A = I_n
Similarly, each of the ![]() is invertible, a series of inverse operation on I will give back
is invertible, a series of inverse operation on I will give back ![]() .
.
A = E^{-1}_1 . E^{-1}_2 ...E^{-1}_nAlso,
A^{-1} = E_1.E_2 ... E_n.ITherefore, the matrix ![]() is product of elementary matrices.
is product of elementary matrices.
Example #8: Find the inverse of following ![]() matrix using Gauss-Jordan elimination method.
matrix using Gauss-Jordan elimination method.
(A|I) = \left(\begin{array}{ccc|ccc}1 & -2 & 1 & 1 & 0 & 0\\6 & 2 & 3 & 0 & 1 & 0\\2 & 1 & 4 & 0 & 0 & 1\end{array} \right)Solution:
Given the matrix ![]() we will find the inverse of matrix
we will find the inverse of matrix ![]() using the Gauss-Jordan elimination method.
using the Gauss-Jordan elimination method.
(A|I) = \left(\begin{array}{ccc|ccc}1 & -2 & 1 & 1 & 0 & 0\\6 & 2 & 3 & 0 & 1 & 0\\2 & 1 & 4 & 0 & 0 & 1\end{array} \right)Step 1: ![]()
= \left(\begin{array}{ccc|ccc}1 & -2 & 1 & 1 & 0 & 0\\6 & 2 & 3 & 0 & 1 & 0\\0 & 5 & 2 & -2 & 0 & 1\end{array} \right)Step 2: ![]()
= \left(\begin{array}{ccc|ccc}1 & -2 & 1 & 1 & 0 & 0\\0 & 14 & -3 & -6 & 1 & 0\\0 & 5 & 2 & -2 & 0 & 1\end{array}\right)Step 3: ![]()
= \left(\begin{array}{ccc|ccc}1 & -2 & 1 & 1 & 0 & 0\\0 & 1 & -3/14 & -6/14 & 1/14 & 0\\0 & 5 & 2 & -2 & 0 & 1\end{array}\right)Step 4: ![]()
= \left(\begin{array}{ccc|ccc}1 & -2 & 1 & 1 & 0 & 0\\0 & 1 & -3/14 & -6/14 & 1/14& 0\\0 & 0 & 43/14&2/14& -5/14 & 1\end{array}\right)Step 5: ![]()
= \left(\begin{array}{ccc|ccc}1 & -2 & 1 & 1 & 0 & 0\\0 & 1 & -3/14 & -6/14&1/14& 0\\0 & 0 & 1 & 2/43 &-5/ 43 &14/43\end{array}\right)Step 6: ![]()
= \left(\begin{array}{ccc|ccc}1 & -2 & 1 & 1 & 0 & 0\\0 & 1 & 0 & -18/43& 2/43 & 3/43\\0 & 0 & 1 & 2/43 & -5/43&14/43\end{array}\right)Step 7: ![]()
= \left(\begin{array}{ccc|ccc}1& 0 & 0 & 7/43& 4/43&6/43\\0 & 1 & 0 &-18/43&2/43& 3/43\\0 & 0 & 1 & 2/43 & -5/43&14/43\end{array}\right)Step 8: ![]()
(I|A^{-1})= \left(\begin{array}{ccc|ccc}1& 0 & 0 & 5/43 &9/43&-8/43\\0 & 1 & 0 & -18/43&2/43 &3/43\\0 & 0 & 1 & 2/43& -5/43 &14/43\end{array}\right)The matrix ![]() is reduced to an identity matrix and the identity matrix after Gauss-Jordan elimination method reduced to inverse matrix of
is reduced to an identity matrix and the identity matrix after Gauss-Jordan elimination method reduced to inverse matrix of ![]() .
.
The verification of resultant inverse matrix is left as an exercise for you.
