The matrices can be multiplied to get product matrix and also they demonstrate all other mathematical properties. The power of matrices is another mathematical property of matrix where matrix is raised to a power using an exponent. This brings another question, does the exponent laws applies to matrices or not ? what type of matrices qualifies to be raised to some power ? What about common mathematical identities that involve matrices and power of matrices.
Exponents or Power of a Number
Exponent or power is a number which tell us how many times a number ![]() should multiplied by itself. If
should multiplied by itself. If ![]() represents a base and
represents a base and ![]() is its power, then its written as
is its power, then its written as ![]() which means
which means

Similarly, a square matrix ![]() and an integer
and an integer ![]() is given, then
is given, then ![]() power of
power of ![]() is defined as product matrix obtained by multiplying
is defined as product matrix obtained by multiplying ![]() by itself
by itself ![]() times.
times.
A^n = A \times A \times A \times ... \times A \hspace{5px}(n \hspace{5px}times)Note that the matrix ![]() is
is
- a square matrix
- and
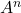 is a product matrix of same order.
is a product matrix of same order.
The exponents have their own algebra which is given as follows.
Basic Laws of Exponents
The basic laws of exponents applied to any real number ![]() and these are
and these are
We need to find out whether these laws applies to square matrices or not. Let us verify this claim with examples.
Example Proof #1
Suppose ![]() is a square matrix of order 2 x 2.
is a square matrix of order 2 x 2.
\begin{aligned}
&A = \begin{bmatrix}1 & 2\\2 & 3\end{bmatrix}\\\\
&A^2 = \begin{bmatrix}1 & 2\\2 & 3\end{bmatrix} \times \begin{bmatrix}1 & 2\\2 & 3\end{bmatrix} = \begin{bmatrix}1+4 & 2+6\\2+6 & 4+9\end{bmatrix} = \begin{bmatrix}5 & 8\\8 & 13\end{bmatrix}\\\\
&A^3 = \begin{bmatrix}5 & 8\\8 & 13\end{bmatrix} \times \begin{bmatrix}1 & 2\\2 & 3\end{bmatrix} = \begin{bmatrix}5+16 & 10+24\\8+26 & 16+39\end{bmatrix} = \begin{bmatrix}21 & 34\\34 & 55\end{bmatrix}\\\\
&A^2 \times A^3 = A^{2 + 3} = A^{5}\\\\
&A^2 \times A^3 = \begin{bmatrix}5 & 8\\8 & 13\end{bmatrix} \times \begin{bmatrix}21 & 34\\34 & 55\end{bmatrix} = \begin{bmatrix}105+272 & 170+440\\168+442 & 272+715\end{bmatrix} = \begin{bmatrix}377 & 610\\610 & 987\end{bmatrix}\\\\
&
\end{aligned}Also,
\begin{aligned}
&A^5 = \begin{bmatrix}377 & 610\\610 & 987\end{bmatrix}
\end{aligned}Therefore, both side of the equation is equal.
Example Proof #2
There is not concept of division in matrix, however, you can divide element of matrix by multiplying it with an inverse value which is same as dividing the element. Inverse of a matrix is covered in the next lesson.
If ![]() is a square matrix of order 2 x 2. Then,
is a square matrix of order 2 x 2. Then,
\begin{aligned}
A = \begin{bmatrix}1 & 2\\2 & 3\end{bmatrix}
\end{aligned}Therefore,
![]() is not possible, but if
is not possible, but if ![]() is an invertible matrix then,
is an invertible matrix then,
\begin{aligned}
A.A^{-1} = I
\end{aligned}Where, ![]() is inverse of the matrix
is inverse of the matrix ![]() of same order and
of same order and ![]() is called the identity matrix of same order.
is called the identity matrix of same order.
Example Proof #3
The power of power of a matrix is a product matrix with exponents multiplied. If ![]() is a square matrix raised to power
is a square matrix raised to power ![]() and
and ![]() is also raised to the power
is also raised to the power ![]() , then the resultant product matrix is
, then the resultant product matrix is ![]() of same order.
of same order.
Let ![]() be a square matrix with order 2 x 2.
be a square matrix with order 2 x 2.
\begin{aligned}
A = \begin{bmatrix}1 & 2\\2 & 3\end{bmatrix}
\end{aligned}Then,
\begin{aligned}
&(A^2)^3 = A^{2 \times 3} = A^6\\\\
&(A^2)^3 = \begin{bmatrix}5 & 8\\8 & 13\end{bmatrix}^3\\\\
&A^{2 \times 3} = \begin{bmatrix}5 & 8\\8 & 13\end{bmatrix} \times \begin{bmatrix}5 & 8\\8 & 13\end{bmatrix} \times \begin{bmatrix}5 & 8\\8 & 13\end{bmatrix}\\\\
&A^{2 \times 3} = \begin{bmatrix}89 & 144\\144 & 233\end{bmatrix} \times \begin{bmatrix}5 & 8\\8 & 13\end{bmatrix}\\\\
&A^{2 \times 3} = \begin{bmatrix}445 + 1152 & 712 + 1872\\720 + 1864 & 1152+3029\end{bmatrix}\\\\
&A^{2 \times 3} = \begin{bmatrix}1597 & 2584\\2584 & 4184\end{bmatrix}\\\\
&Also,\\\\
&A^6 = \begin{bmatrix}1597 & 2584\\2584 & 4184\end{bmatrix}
\end{aligned}Example Proof #4
The product of defined matrices ![]() raised to power
raised to power ![]() is equal to product of powers of individual matrices
is equal to product of powers of individual matrices ![]() and
and ![]() raised to the power
raised to the power ![]() .
.
\begin{aligned}
&(AB)^p = A^p \times B^p\\\\
\end{aligned}We can rewrite the equation as
\begin{aligned}
&(AB)^p = (AB)(AB)(AB)... p-times\\\\
&(AB)^p = A(BA)(BA)B ... p-times
\end{aligned}But we know that ![]() is not commutative.
is not commutative.
\begin{aligned}
AB \ne BA
\end{aligned}Therefore,
\begin{aligned}
(AB)^p \ne A^p \times B^p
\end{aligned}Why Only Square Matrix ?
Only square matrix is suitable for exponents or to be raised to some powers because of two reasons.
- Non-Square or Singular matrices are not defined. If
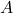 is a non-square matrix of order
is a non-square matrix of order 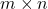 then
then 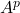 is not possible because
is not possible because 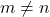 where
where 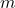 is row and
is row and 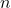 is column of matrix
is column of matrix 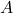 .
. - When we need to take inverse which is
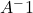 , the matrix must be a square. Singular matrices are not invertible.
, the matrix must be a square. Singular matrices are not invertible.
Example Proof #5
Let ![]() be a non-square matrix with order
be a non-square matrix with order ![]() . Let
. Let ![]() be an non-negative integer whose value is 2.
be an non-negative integer whose value is 2.
\begin{aligned}
&A = \begin{bmatrix}1 & 4 & 2\\2 & 0 & 1\end{bmatrix}\\\\
\end{aligned}Let us try to obtain ![]() , then we observe that it is not possible.
, then we observe that it is not possible.
![]() is undefined where
is undefined where ![]() and
and ![]() . This is because
. This is because ![]() required for multiplication of matrices.
required for multiplication of matrices.
Therefore, a matrix cannot be raised to power unless it is a square matrix.
Example Proof #6
Another reason to use square matrix with power is to find inverse matrix. If ![]() is a matrix that is invertible and we wish to find the inverse matrix
is a matrix that is invertible and we wish to find the inverse matrix ![]() such that
such that
\begin{aligned}
A.A^{-1} = A^{-1}.A = I_{n \times n}
\end{aligned}The ![]() represents an identity matrix whose main diagonals are 1 and rest of the entries are 0. It is a square matrix. Therefore,
represents an identity matrix whose main diagonals are 1 and rest of the entries are 0. It is a square matrix. Therefore, ![]() and
and ![]() must be square matrices.
must be square matrices.
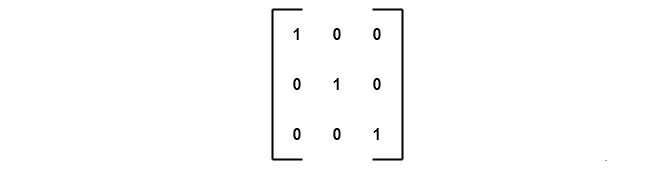
 square matrix.
square matrix.In the next section, we will explore whether matrices complies with common algebraic identities or not.
Common Algebraic Identities And Square Matrices
The standard algebraic identities are true for any value of variables. Instead of numbers, we will use square matrix to prove these identities holds for matrices too.
Order Of Multiplication
In matrix multiplication, the order of multiplication is very important because ![]() which is even true for square matrices.
which is even true for square matrices.
If ![]() , then any one of the following is true.
, then any one of the following is true.
- The matrix
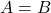 .
. - Either
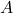 or
or 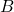 is identity matrix
is identity matrix 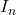 .
. - Either
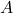 or
or 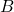 is zero or null matrix
is zero or null matrix 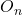 .
. - The
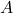 is inverse of
is inverse of 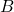 or the matrix
or the matrix 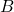 is inverse of
is inverse of 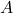 .
.
Let us now verify the common algebraic identities with matrices as variables.
Example Proof #7
We check the following identity : ![]() .
.
Let ![]() and
and ![]() be square matrices of order 2 x 2.
be square matrices of order 2 x 2.
\begin{aligned}
&(A + B)^2 = (A + B)(A + B)\\\\
&= A^2 + AB + BA + B^2
\end{aligned}But ![]() , therefore,
, therefore,
![]() not possible.
not possible.
Example Proof #8
We will verify the claim: ![]()
Let ![]() and
and ![]() be square matrix of order 2 x 2.
be square matrix of order 2 x 2.
\begin{aligned}
&A^2 - B^2 = (A + B)(A - B)\\\\
&
\end{aligned}We can write the right-hand side as,
\begin{aligned}
&= A^2 - AB + BA - B^2
\end{aligned}But we know that ![]() , therefore, above identity is false.
, therefore, above identity is false.
Example Proof #9
We check the identity: ![]() .
.
Let ![]() and
and ![]() be square matrices of order 2 x 2. We multiply (A + B)^3, we get following results.
be square matrices of order 2 x 2. We multiply (A + B)^3, we get following results.
\begin{aligned}
&(A + B)(A + B)(A + B)
\end{aligned}Since, we know that ![]() is not possible. Therefore,
is not possible. Therefore, ![]() is also false.
is also false.
Example Proof #10
We now verify the identity : ![]()
Let ![]() and
and ![]() be square matrices and single both are defined. We get following equation from $A^2B^2.
be square matrices and single both are defined. We get following equation from $A^2B^2.
\begin{aligned}
&A^2B^2 = A.A.B.B
\end{aligned}We get,
\begin{aligned}
A^2B^2 = A(A.B)B
\end{aligned}Therefore, the identity is true because the order of multiplication is same.
