Triangular matrices are diagonal matrix plus some elements on the upper side or lower side of the main diagonal. Here we discuss about types, interesting properties of triangular matrix. Later we will find ways to determine the invertibility and how to find inverse of a triangular matrix with examples.
What Are Triangular Matrices ?
If a square matrix has all zeros below its main diagonal entries then it is called upper triangular matrix and if the square matrix has all zeros above the main diagonal entries then it is called lower triangular matrix. Therefore, a triangular matrix has either all zero entries above or below main diagonal.
Examples of Upper Triangular Matrix
\begin{aligned}
&A = \begin{bmatrix}a_{11} & a_{12}\\0 & a_{22}\end{bmatrix}\\\\
&B = \begin{bmatrix}a_{11} & a_{12}& a_{13}\\0 & a_{22}& a_{23}\\0 & 0 & a_{33}\end{bmatrix}\\\\
&C = \begin{bmatrix}2 & 1 & 9 & 3\\0 & -1 & 8 &-2\\0 & 0 & -7 & 5\\0& 0 & 0 & 4\end{bmatrix}
\end{aligned}Examples of Lower Triangular Matrix
\begin{aligned}
&P = \begin{bmatrix}a_{11} & 0\\a_{12} & a_{22}\end{bmatrix}\\\\
&Q = \begin{bmatrix}a_{11} & 0& 0\\a_{21} & a_{22}& 0\\a_{31} & a_{32} & a_{33}\end{bmatrix}\\\\
&R = \begin{bmatrix}-1 & 0 & 0 & 0\\5 & 1 & 0 &0\\-3 & 1 & -7 & 0\\8& 2 & -6 & 2\end{bmatrix}
\end{aligned}Rules Regarding Triangular Matrices
Here are some basic rules regarding the upper or lower triangular matrices.
- If a square matrix
![Rendered by QuickLaTeX.com A= [a_{ij}]](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-7f076d74750b3d1384cd7ce5883a7eb0_l3.png) is upper triangular matrix then
is upper triangular matrix then 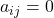 and
and 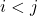 .
. - If a square matrix
![Rendered by QuickLaTeX.com A= [a_{ij}]](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-7f076d74750b3d1384cd7ce5883a7eb0_l3.png) is lower triangular matrix then
is lower triangular matrix then 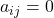 and
and 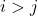 .
. - If a square matrix
![Rendered by QuickLaTeX.com A= [a_{ij}]](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-7f076d74750b3d1384cd7ce5883a7eb0_l3.png) is upper triangular matrix then
is upper triangular matrix then 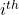 row has and starts with
row has and starts with 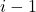 zeros.
zeros. - If a square matrix
![Rendered by QuickLaTeX.com A= [a_{ij}]](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-7f076d74750b3d1384cd7ce5883a7eb0_l3.png) is lower triangular matrix then
is lower triangular matrix then 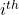 row has and starts with
row has and starts with  zeros.
zeros.
Strict Triangular Matrix
A strict triangular matrix is a square matrix which has all entries zero below or above the main diagonal including the main diagonal.
Strict Upper Triangular Matrix
If a strict triangular matrix has all zero entries below the main diagonal including the main diagonal then it is called strict upper triangular matrix.
Example of Strict Upper Triangular Matrix
\begin{aligned}
&A = \begin{bmatrix}0 & b\\0 & 0\end{bmatrix}\\\\
&B = \begin{bmatrix}0 & 4 & 2\\0 & 0 & 1\\0 & 0 & 0\end{bmatrix}
\end{aligned}Examples of Strict Lower Triangular Matrix
\begin{aligned}
&C = \begin{bmatrix}0 & 0\\c & 0\end{bmatrix}\\\\
&D = \begin{bmatrix}0 & 0 & 0\\7 & 0 & 0\\3 & 9 & 0\end{bmatrix}
\end{aligned}The basic rules for constructing strict upper or strict lower triangular matrix are
- If a square matrix
![Rendered by QuickLaTeX.com A = [a_{ij}]](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-225992b3722a8cd74c51719d967f6b9e_l3.png) is strict upper triangular matrix when
is strict upper triangular matrix when 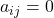 and
and 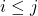 .
. - If a square matrix
![Rendered by QuickLaTeX.com A = [a_{ij}]](https://notesformsc.org/wp-content/ql-cache/quicklatex.com-225992b3722a8cd74c51719d967f6b9e_l3.png) is strict lower triangular matrix when
is strict lower triangular matrix when 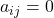 and
and 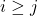 .
.
Properties Of Triangular Matrix
There are some interesting properties of triangular matrices which we will explore each type of triangular matrices with examples.
Properties of Upper Triangular Matrices
The upper triangular matrix is in row-echelon form. Here are the properties of upper triangular matrices.
- Adding two upper triangular matrices of same order will result in a upper triangular matrix of same order.
- Product of two defined ( eligible for multiplication) upper triangular matrices is upper triangular matrix.
- Transpose of upper triangular matrix is lower triangular matrix.
- Inverse of upper triangular matrix is also upper triangular matrix.
Let us verify each claim with examples.
Addition of Two Upper Triangular Matrices
Let ![]() and
and ![]() be two upper triangular matrices of order
be two upper triangular matrices of order ![]() .
.
\begin{aligned}
&A = \begin{bmatrix}2 & 3 & 5\\0 & 3 & 6\\0 & 0 & 1\end{bmatrix} \hspace{5px} B = \begin{bmatrix}6 & 1 & 7\\0 & 4 & 1\\0 & 0 & 8\end{bmatrix}\\\\
&A + B = \begin{bmatrix}8 & 4 & 12\\0 & 7 & 7\\0 & 0 & 9\end{bmatrix}
\end{aligned}Therefore, sum of two upper triangular matrices is an upper triangular matrix.
Product of Two Upper Triangular Matrix
Let ![]() and
and ![]() be two matrices of order
be two matrices of order ![]() .
.
\begin{aligned}
&C = \begin{bmatrix}2 & 7\\0 & 4\end{bmatrix}\\\\
&D = \begin{bmatrix}1 & 3\\0 & 5\end{bmatrix}
\end{aligned}Let the product of ![]() .
.
\begin{aligned}
&K = \begin{bmatrix}2+0 & 6+35\\0+0 & 0+20\end{bmatrix}\\\\
&K = \begin{bmatrix}2 & 41\\0 & 20\end{bmatrix}
\end{aligned}The product of two defined upper triangular matrices is an upper triangular matrix.
Transpose of Upper Triangular Matrix
The transpose of a matrix can be obtained by changing all rows into columns or all columns into rows.
A = \begin{bmatrix}a & b & c\\0 & d & e\\0 & 0 & f\end{bmatrix}Then the transpose of matrix ![]() is
is
A^T = \begin{bmatrix}a & 0 & 0\\b & d & 0\\c & e & f\end{bmatrix}Inverse of Upper Triangular Matrix
Like diagonal matrix, if the main diagonal of upper triangular matrix is non-zero then it is invertible. To be invertible a square matrix must has determinant not equal to 0. Since, determinant of a upper triangular matrix is product of diagonals if it is nonzero, then the matrix is invertible.
Let ![]() be a upper triangular matrix of order
be a upper triangular matrix of order ![]() .
.
A = \begin{bmatrix}2 & 5\\0 & 3\end{bmatrix} The determinant is nonzero, therefore, matrix ![]() is invertible.
is invertible.
\begin{aligned}
&|A| = 2 \times 3 = 6\\\\
&A^{-1} = 1/6 \times \begin{bmatrix}3 & -5\\0 & 2\end{bmatrix}\\\\
&A^{-1} = \begin{bmatrix}1/2& -5/ 6\\0 &1/3\end{bmatrix}
\end{aligned}Properties of Lower Triangular Matrices
The properties of lower triangular matrices are similar to that of upper triangular matrices,but we decided to discuss it separately. Here are the basic properties
- Adding two lower triangular matrices of same order will result in a lower triangular matrix of same order.
- Product of two defined ( eligible for multiplication) lower triangular matrices is lower triangular matrix.
- Transpose of lower triangular matrix is upper triangular matrix.
- Inverse of lower triangular matrix is also lower triangular matrix.
Let us verify each statement with examples.
Addition of Lower Triangular Matrix
Let ![]() and
and ![]() be two lower triangular matrices of order
be two lower triangular matrices of order ![]() .
.
A = \begin{bmatrix}2 & 0 & 0\\4 & 1 & 0\\3 & 9 & 5\end{bmatrix} \hspace{5px} B = \begin{bmatrix}-3 & 0 & 0\\-2 & 7 & 0\\-1 & 6 & 1\end{bmatrix}The addition of matrix is stored in matrix ![]() .
.
\begin{aligned}
&C = A + B\\\\
&C = \begin{bmatrix}2 & 0 & 0\\4 & 1 & 0\\3 & 9 & 5\end{bmatrix} + \begin{bmatrix}-3 & 0 & 0\\-2 & 7 & 0\\-1 & 6 & 1\end{bmatrix}\\\\
&C = \begin{bmatrix}-1 & 0 & 0\\2 & 8 & 0\\2 & 15 & 6\end{bmatrix}
\end{aligned}Therefore, above results shows that sum of two lower triangular matrix is a lower triangular matrix of same order.
Product of Two Lower Triangular Matrix
Similar to upper triangular matrix, the product of two defined lower triangular matrix is a lower triangular matrix.
Let ![]() and
and ![]() be two lower triangular matrix of order
be two lower triangular matrix of order ![]() and the product matrix is
and the product matrix is ![]() of same order.
of same order.
\begin{aligned}
&A = \begin{bmatrix}6 & 0 & 0\\2 & 7 & 0\\1 & 9 & 3\end{bmatrix} \hspace{5px} B = \begin{bmatrix}-1 & 0 & 0\\5 & 3 & 0\\-3 & 2 & -5\end{bmatrix}\\\\
&C = A \times B\\\\
&C = \begin{bmatrix}-6 & 0 & 0\\33 & 21 & 0\\35 & 33 & -15\end{bmatrix}
\end{aligned}Transpose of Lower Triangular Matrix
The transpose of lower triangular matrix will change all rows to columns or columns to rows which result in an upper triangular matrix. Consider the following example.
Let ![]() be a lower triangular matrix of order
be a lower triangular matrix of order ![]() . The transpose of matrix
. The transpose of matrix ![]() is denoted as
is denoted as ![]() .
.
S = \begin{bmatrix}2 & 0 & 0 & 0\\7 & 5 & 0 & 0\\1 & 3 & 2 & 0\\4 & 9 & 6 & 8\end{bmatrix}Transpose of matrix ![]() .
.
S^T = \begin{bmatrix}2 & 7 & 1 & 4\\0 & 5 & 3 & 9\\0 & 0 & 2 & 6\\0 & 0 & 0 & 8\end{bmatrix}Inverse of Lower Triangular Matrix
The invertibility requirement of lower triangular matrix is same as that of upper triangular matrix. The main diagonal element should not be zero because the determinant of the lower triangular matrix must not be a zero; otherwise there is no inverse matrix.
Let ![]() be a lower triangular matrix of order
be a lower triangular matrix of order ![]() .
.
L = \begin{bmatrix}2 & 0 & 0 &0\\3 & 1 & 0 & 0\\2 & 5 & 6 & 0\\4 & 3 & 2 & 7\end{bmatrix}Since the diagonals are non-zero, the matrix ![]() is invertible and its determinant is
is invertible and its determinant is ![]() .
.
|L| = 2 \times 1 \times 6 \times 7 = 84
The minor matrix of ![]() .
.
\begin{aligned}
&M_{11} = \begin{vmatrix}1 & 0 & 0\\5 & 6 & 0\\3 & 2 & 7\end{vmatrix} = 42, M_{12} = \begin{vmatrix}3 & 0 & 0\\2 & 6 & 0\\4 & 2 & 7\end{vmatrix} = 126\\\\
&M_{13} = \begin{vmatrix}3 & 1 & 0\\2 & 5 & 0\\4 & 3 & 7\end{vmatrix} = 91, M_{14} = \begin{vmatrix}3 & 1 & 0\\2 & 5 & 6\\4 & 3 & 2\end{vmatrix} = -4\\\\
&M_{21} = \begin{vmatrix}0 & 0 & 0\\5 & 6 & 0\\3 & 2 & 7\end{vmatrix} = 0, M_{22} = \begin{vmatrix}2 & 0 & 0\\2 & 6 & 0\\4 & 2 & 7\end{vmatrix} = 84\\\\
&M_{23} = \begin{vmatrix}2 & 0 & 0\\2 & 5 & 0\\4 & 3 & 7\end{vmatrix} = 70, M_{24} = \begin{vmatrix}2 & 0 & 0\\2 & 5 & 6\\4 & 3 & 2\end{vmatrix} = -16\\\\
&M_{31} = \begin{vmatrix}0 & 0 & 0\\1 & 0 & 0\\3 & 2 & 7\end{vmatrix} = 0, M_{32} = \begin{vmatrix}2 & 0 & 0\\3 & 0 & 0\\4 & 2 & 7\end{vmatrix} = 0\\\\
&M_{33} = \begin{vmatrix}2 & 0 & 0\\3 & 1 & 0\\4 & 3 & 7\end{vmatrix} = 14, M_{34} = \begin{vmatrix}2 & 0 & 0\\3 & 1 & 0\\4 & 3 & 2\end{vmatrix} = 4\\\\
&M_{41} = \begin{vmatrix}0 & 0 & 0\\1 & 0 & 0\\5 & 6 & 0\end{vmatrix} = 0, M_{42} = \begin{vmatrix}2 & 0 & 0\\3 & 0 & 0\\2 & 6 & 0\end{vmatrix} = 0\\\\
&M_{43} = \begin{vmatrix}2 & 0 & 0\\2 & 5 & 0\\4 & 3 & 7\end{vmatrix} = 0, M_{44} = \begin{vmatrix}2 & 0 & 0\\3 & 1 & 0\\2 & 5 & 6\end{vmatrix} = 12\\\\
&= \begin{bmatrix}42 & 126 & 91 & -4\\0 & 84 & 70 & -16\\0 & 0 & 14 & 4\\0 & 0 & 0 & 12\end{bmatrix}
\end{aligned}From the minor matrix we can obtain the cofactor matrix. Each cofactor value can be obtained using
\begin{aligned}
&L_{ij} = (-1)^{i+j} \times M_{ij}\\\\
&= \begin{bmatrix}42 & -126 & 91 & 4\\0 & 84 & -70 & -16\\0 & 0 & 14 & -4\\0 & 0 & 0 & 12\end{bmatrix}
\end{aligned}The adjoint matrix can be obtained from the cofactor matrix and we can find the inverse of the matrix.
Adj \hspace{3px} L = \begin{bmatrix}42 & 0 & 0 & 0\\-126 & 84 & 0 & 0\\91 & -70 & 14 & 0\\4 & -16 & -4 & 12\end{bmatrix} Therefore, The inverse of matrix ![]() is
is ![]() and obtained using
and obtained using
\begin{aligned}
&L^{-1} = 1/84 \times Adj \hspace{3px}L\\\\
&L^{-1} = 1/84 \times \begin{bmatrix}42 & 0 & 0 & 0\\-126 & 84 & 0 & 0\\91 & -70 & 14 & 0\\4 & -16 & -4 & 12\end{bmatrix}\\\\
&L^{-1} = \begin{bmatrix}1/2& 0 & 0 & 0\\ -3/2& 1 & 0 & 0\\91/84&-5/6&1/6& 0\\1/21& -4/21& -1/ 21&1/7\end{bmatrix}
\end{aligned}Therefore, lower triangular matrix has a lower triangular inverse matrix. Let us verify the inverse matrix.
\begin{aligned}
&L \times L^{-1} = I\\\\
&= \begin{bmatrix}2 & 0 & 0 &0\\3 & 1 & 0 & 0\\2 & 5 & 6 & 0\\4 & 3 & 2 & 7\end{bmatrix} \times \begin{bmatrix}1/2& 0 & 0 & 0\\ -3/2& 1 & 0 & 0\\91/84&-5/6 &1/6& 0\\1/21& -4/21& -1/21&1/7\end{bmatrix}\\\\
&= \begin{bmatrix}1 & 0 & 0 &0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{bmatrix}
\end{aligned}In the next article, we will discuss some interesting way to solve Ax = b using triangular matrices.
