Cramer’s rule is a method of solving the system of linear equations using determinants. It is named after Gabriel Cramer (1704–1752) who discovered this method. In this article we are going to discuss and work few examples for solving system of linear equations using Cramer’s rule.
Before you start reading about Cramer’s rule, learn to compute determinant of 2 x 2 and 3 x 3 matrix as a prerequisite to this article : Finding Determinants Using Cross Multiplication.
Coefficient Matrix and Augmented Matrix
Given a system of equation you can derive a coefficient matrix and an augmented matrix from it. Both are the same thing with little different.
Suppose you are given a system of linear equations with 2 unknowns.
\begin{aligned}
&a_{11}x + a_{12}y = b_1\\\\
&a_{21}x + a_{22}y = b_2
\end{aligned}The augmented matrix and coefficient matrix would look like the following.
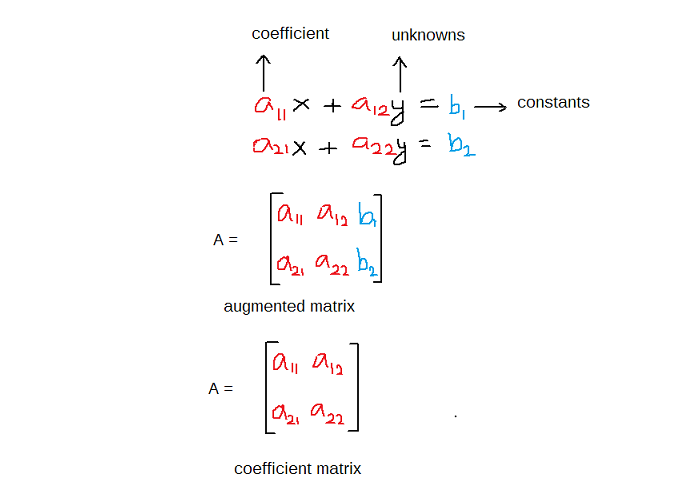
The system of linear equation is in the form of 
which is written as
\begin{aligned}
&Ax = b\\\\
&\begin{bmatrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{bmatrix} . \begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix}b_1 \\ b_2\end{bmatrix}
\end{aligned}The matrix 
is coefficient matrix, 
is a column vector of unknowns, and 
represents the constant vector.
Determinant Of 2 x 2 Matrix
The determinant of a 2 x 2 matrix can be calculated using cross multiplication.
\begin{aligned}
&A = \begin{bmatrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{bmatrix}\\\\
&|A| = \begin{vmatrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{vmatrix} = a_{11}a_{22} - a{12}.a_{21}
\end{aligned}Example #1
Find the determinant of 
.
Solution:
|A|= \begin{vmatrix}2 & 1\\3 & 7\end{vmatrix} = 14 - 3 = 11Solving System of Equations with 2 Unknowns With Cramer’s Rule
Given a system of equations with 2 unknowns you can solve it using Cramer’s rule by following steps.
- Find the augmented matrix and the coefficient matrix for the system of equations.
- Find the determinant of
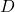of matrix . - Replace the 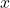coefficients of coefficient matrix with constant vector 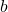to get x-matrix and find its determinant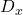
- Replace the
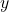coefficients of coefficient matrix with constant vector 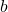to get y-matrix and find its determinant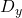 
- Find the solution to system of linear equation according to following equations.
\begin{aligned}
&x = D_x/D\\\\
&y = D_y/D
\end{aligned}See the following figure to understand how the matrices look like.
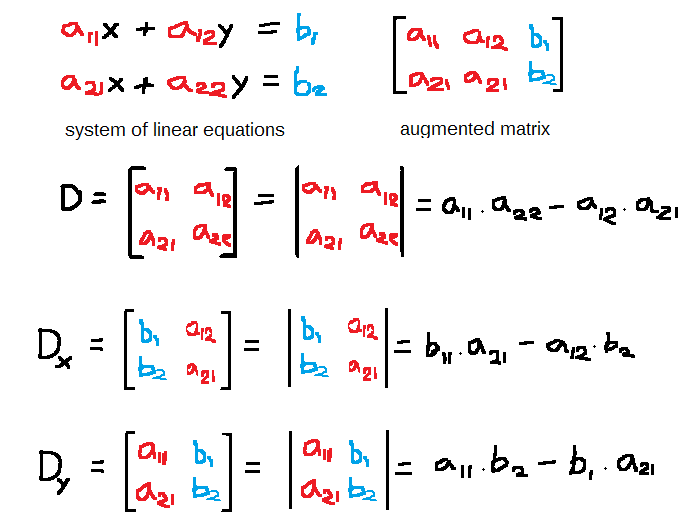
Given a system of equations such as shown above, first derive the augmented matrix and coefficient matrix. The coefficient matrix has no constant vector. Use the coefficient matrix to get the determinant of matrix which is .
X Matrix And Y Matrix
You can get x matrix by replacing the first column which is x column by the constant vector. See the image below.
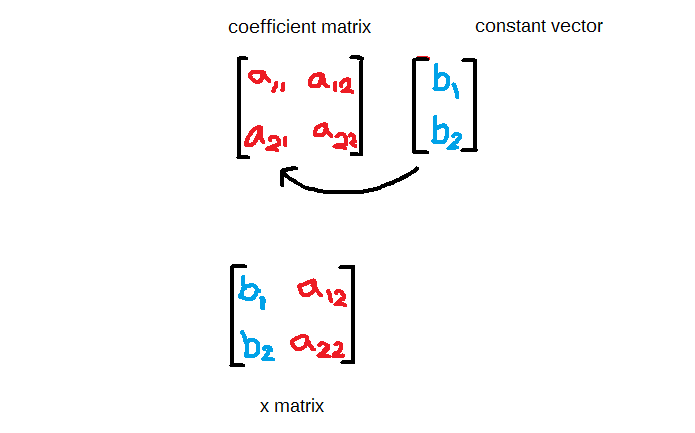
Similarly, compute the y matrix from coefficient matrix of . Compute the determinant of x matrix which is and compute the determinant of y matrix which is .
To find the solution to each unknowns use the following formula, mentioned earlier.
Solution for x
\begin{aligned}
&x = D_x/D
\end{aligned}Solution for y,
y = D_y/D
In the next section, we will solve a system of linear equation with two unknown.
Example #1
Find the solution to following system of linear equations with two unknowns using Cramer’s rule.
\begin{aligned}
&x + 3y = 5\\\\
&5x - 2y = 8
\end{aligned}Solution:
Given the system of linear equations we can obtain augmented matrix and coefficient matrix.
A = \begin{bmatrix}1 & 3 & 5\\5 & -2 & 8\end{bmatrix}The coefficient matrix must be a square matrix, so lets write the augmented matrix in the form in that order.
\begin{aligned}
&Ax = b\\\\
&\begin{bmatrix}1& 3\\5 & -2\end{bmatrix} . \begin{bmatrix}x & y\end{bmatrix} = \begin{bmatrix}5 & 8\end{bmatrix}
\end{aligned}Compute the determinant of the matrix .
D = \begin{vmatrix}1& 3\\5 & -2\end{vmatrix} = -2 - 15 = -17 Compute the determinant of the matrix.
D_x = \begin{vmatrix}5 & 3\\8 & -2\end{vmatrix} = -10 - 24 = -34 Compute the determinant of the matrix.
D_y = \begin{vmatrix}1& 5\\5 & 8\end{vmatrix} = 8 - 25 = -17Therefore,
\begin{aligned}
&x = -34/(-17) = 2\\\\
&y = -17/(-17)= 1
\end{aligned}We can verify the solution by substitution.
\begin{aligned}
&(2) + 3(1) = 5\\\\
&5(2) - 2(1) = 8
\end{aligned}The solutions to the system of linear equations are correct.
Solving System Of Equations With 3 Unknowns Using Cramer’s Rule
We can solve the system of equations with 3 unknowns which gives a 
square matrix using the Cramer’s rule.
Though we need to compute the determinant of additional sub-matrices because there is one more unknown other than x and y. Let us call it z.
The steps remain the same as we solved for 
matrix. Here is the list of steps.
Let be a matrix.
Step 1: Compute determinant of .
Step 2: You must extract sub-matrices or minors from the matrix and take determinant
