So far you have learned about non-homogeneous system of linear equations of the form 
where 
is the augmented matrix and 
is the matrix representing unknowns and 
is the result of the product. The homogeneous system of linear equations has all of its constant term set to zero.
Consider the following homogeneous system of linear equation.
\begin{aligned}
&A = \begin{bmatrix}2 & 4 \\1 & 3\end{bmatrix} X = \begin{bmatrix}x\\y\end{bmatrix} B = \begin{bmatrix}0\\0\end{bmatrix}\\\\
&A \cdot X = \begin{bmatrix}2 & 4 \\1 & 3\end{bmatrix} \cdot \begin{bmatrix}0\\0\end{bmatrix}= \begin{bmatrix}0\\0\end{bmatrix} = B
\end{aligned}Consistent System
The homogeneous system of linear equations is a consistent with at least one solution. It is called the trivial solution. Let there be a homogeneous system of linear equations with two unknown variable.
\begin{aligned}
&2x + y = 0\\\\
&x + \frac{1}{2}y = 0
\end{aligned}The system has solution when 
and 
.
\begin{aligned}
&2(0) + (0) = 0\\\\
&(0) + \frac{1}{2}(0) = 0
\end{aligned}Therefore, 
is a trivial solution to homogeneous system of linear equations.
Non-Trivial Solution To Homogeneous Equations
The homogeneous system is consistent so there are two possibilities.
- It has only trivial solution
- It has infinite many solutions including trivial solution.
Graphical Representation
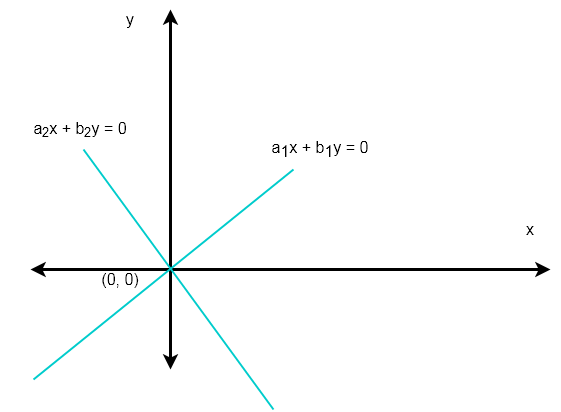
Suppose there are two lines
\begin{aligned}
&a_1x + b_1y = 0\\\\
&a_2x + b_2y = 0
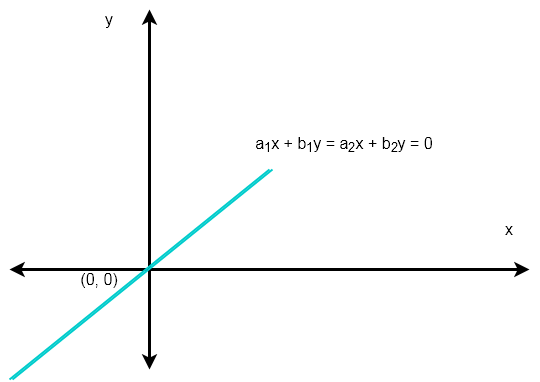
\end{aligned}When two lines intersect at a single point there is only one unique solution. In the case of homogeneous linear equations the point of interaction is the origin 
.
If the homogeneous system linear equations has 
equations with 
unknowns where 
then we can say that it is guaranteed to have a non-trivial solutions.
To solve a system of linear equation we perform Gauss-Jordan elimination and the augmented matrix is reduced to echelon form or reduced row echelon form. We use the same elimination technique to reduce the homogeneous system of linear equations. For example, consider following homogeneous system of linear equations.
\begin{aligned}
&x_2 + x_4 = 0\\\\
&x_1 - x_3 + x_4 = 0\\\\
&2x_3 - 2x_4 = 0
\end{aligned}From the above homogeneous system of linear equations we obtained following augmented matrix.
\begin{aligned}
A = \begin{bmatrix}2 & -1 & 0 & 1 & 0\\1 & 0 & -1 & 1 & 0\\0 & 0 & 2 & -2 & 0\end{bmatrix}
\end{aligned}Perform the Gauss-Jordan Elimination on the matrix
\begin{aligned}
&R3 = \frac{R3}{2}
\end{aligned}\begin{aligned}
&A = \begin{bmatrix}2 & -1 & 0 & 1 & 0\\1 & 0 & -1 & 1 & 0\\0 & 0 & 1 & -1 & 0\end{bmatrix}
\end{aligned}\begin{aligned}
R1 \longleftrightarrow R2
\end{aligned}\begin{aligned}
&A = \begin{bmatrix}1 & 0 & -1 & 1 & 0\\2 & -1 & 0 & 1 & 0\\0 & 0 & 1 & -1 & 0\end{bmatrix}
\end{aligned}\begin{aligned}
R2 = R2 - 2R1
\end{aligned}\begin{aligned}
&A = \begin{bmatrix}1 & 0 & -1 & 1 & 0\\0 & -1 & 2 & -1 & 0\\0 & 0 & 1 & -1 & 0\end{bmatrix}
\end{aligned}The matrix is in echelon form and we obtained new homogeneous system of linear equations.
\begin{aligned}
&x_1 - x_3 + x_4 = 0\\\\
& -x_2 + 2x_3 - x_4 = 0\\\\
&x_3 - x_4 = 0
\end{aligned}The first variable in each equation is called basic variable and other variables are free variables.
Let basic variables be 
and free variables be 
for 
.
\begin{aligned}
b_n = \sum f_1 + f_2 ... f_n
\end{aligned}Using the above, the reduced form of homogeneous system of linear equation becomes
\begin{aligned}
&x_1 = x_3 - x_4\\\\
&x_2 = 2x_3 - x_4\\\\
&x_3 = x_4\\\\
&x_4 = c
\end{aligned}Therefore, the general solution for the given homogeneous system of linear equation is
\begin{aligned}
&x_1= x_3 - c\\\\
&x_2= 2x_3 - c\\\\
&x_3 = c\\\\
&x_4 = c
\end{aligned}We can make few conclusions based on the example above.
- The echelon form of a homogeneous system of linear equations is also a homogeneous linear equations.
- The non-trivial solution is possible, if m equations and n unknowns with m <= n and after the matrix A is reduced to echelon form with t non-zero rows obtained where t < n.
Relationship Between Non-Homogeneous System And Homogeneous System
There is a relationship between non-homogeneous system of linear equations and homogeneous systems which allows to obtain all solutions to non-homogeneous systems.
Let be a matrix of size 
and 
be a column matrix of size 
such that 
is consistent with a solution 
Then every solution 
can be written as
s = s_1 + p
where p is solution to homogeneous system of linear equations 
which means 
.
This kind of solution is obtained by linear translations about which you will learn in future articles.
