Matrix Multiplication

Table of Contents

The multiplication of matrices means rows of matrix $A$ is multiplied to columns of $B$ to obtain a third matrix $C$ . We also evaluate the matrix multiplication with respect to fundamental properties of mathematics such as commutative, associative property, identity property.

Conditions for Matrix Multiplication

If $A_{m \times n}$ and $B_{n \times p}$ are two matrices with sizes $m \times n$ and $n \times p$ respectively. The following conditions apply to matrix multiplication,

Row or column of matrix 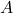$A$ must be equal to column or row of matrix $B$ .
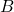Multiplying matrix 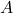$A$ to matrix 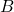$B$ is not same as multiplying matrix 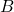$B$ i.e., $AB \neq BA$ .
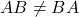If condition 2 and 3 are true, then we can multiply 2 or more matrices.

Matrix Multiplication

Let $A_{1 \times n}$ and $B_{n \times 1}$ be two matrices with elements. Then the matrix multiplication can be done as follows.

\begin{aligned} &A = \begin{bmatrix}a_{11} & a_{12}& . . . & a_{1n}\end{bmatrix} B = \begin{bmatrix}b_{11} \\ b_{21} \\ : \\ b_{n1}\end{bmatrix}\\\\ &C_{1 \times 1} = A . B = \begin{bmatrix}a_{11}b_{11} + a_{12}b_{21} + ... + a_{1n}b_{n1}\end{bmatrix} \end{aligned}

In the above example, $A$ has size $m \times n$ where $m = 1$ and $B$ has size $n \times p$ where the resultant matrix $C$ has size of $m \times p$ which is $1 \times 1$ .

Now, we consider the second case, where we multiply $B$ to $A$ .

\begin{aligned} &B = \begin{bmatrix}b_{11} \\ b_{21} \\ : \\ b_{n1}\end{bmatrix} A = \begin{bmatrix}a_{11} & a_{12}& . . . & a_{1n}\end{bmatrix}\\\\ &C_{n \times n} = A . B = \begin{bmatrix}b_{11}a_{11} & b_{11}a_{12} & ... & b_{11}a_{1n}\\ b_{21}a_{11} & b_{21}a_{11} & ... & b_{21}a_{1n}\\ : & : & : & :\\ b_{n1}a_{11} & b_{n1}a_{12} & ... & b_{n1}a_{1n}\end{bmatrix} \end{aligned}

Matrix Multiplication Examples

In this section, we will show you few examples with different kinds of matrices.

Example #1

\begin{aligned} &// \hspace{5px} Multiplying \hspace{5px} Square \hspace{5px}Matrix\\\\ &A_{2 \times 2} = \begin{bmatrix}2 & 3 \\ 1 & 7\end{bmatrix} B_{2 \times 2} = \begin{bmatrix}2 & 3\\ 1 & 1\end{bmatrix}\\\\ &AB = \begin{bmatrix}(2 * 2)+ (3 * 1) & (2 * 3)+ (3 * 1)\\ (1 * 2) + (7 * 1) & (1 * 3) + ( 7 * 1)\end{bmatrix}\\\\ &AB = \begin{bmatrix}(4)+ (3) & (6)+ (3)\\ (2) + (7) & (3) + (7)\end{bmatrix}\\\\ &AB_{2 \times 2} = \begin{bmatrix}7 & 9\\ 9 & 10\end{bmatrix} \end{aligned}

The size of matrix $A$ is $m \times n$ where $m = n$ and size of matrix $B$ is also $n \times p$ where $n = p$ . Therefore, resultant matrix after multiplication has a size of $m \times p$ where $m = p$ . In other words, $A_{2 \times 2} \times B_{2 \times 2} = C_{2 \times 2}$ .

Example #2

\begin{aligned} &A_{2 \times 3} = \begin{bmatrix}4 & -1 & 1\\ 4 & 1 & -2\end{bmatrix} B_{3 \times 2} = \begin{bmatrix}2 & -2\\ 1 & -2 \\ 5 & 2\end{bmatrix}\\\\ &AB = \begin{bmatrix}(4 * 2)+ (-1 * 1) + (1 * 5) & (4 * -2)+ (-1 * -2) + (1 * 2)\\ (4 * 2) + (1 * 1) + (-2 * 5) & (4 * -2) + ( 1 * -2) + (-2 * 2)\end{bmatrix}\\\\ &AB = \begin{bmatrix}(8)+ (-1) + (5) & (-8)+ (2) + (2)\\ (8) + (1) + (-10) & (-8) + (-2) + (-4)\end{bmatrix}\\\\ &AB = \begin{bmatrix}12 & -4\\ -1 & -14\end{bmatrix} \end{aligned}

The size of the matrix $A$ is $m \times n$ where $m = 2$ and the size of the matrix $B$ is $n \times p$ where $p = 2$ . Therefore, the resultant matrix $AB$ has a size of $m \times p$ which is $2 \times 2$ .

Example #3

\begin{aligned} &A_{3 \times 2} = \begin{bmatrix}1 & 1 \\ 3 & 5 \\ 2 & 3\end{bmatrix} B_{2 \times 3} = \begin{bmatrix}3 & 1 & 0\\ 7 & 4 & 1 \end{bmatrix}\\\\ &AB = \begin{bmatrix}(1 * 3)+ (1 * 7) & (1 * 1) + (1 * 4) & (1 * 0) + (1 * 1)\\ (3 * 3)+ (5 * 7) & (3 * 1) + (5 * 4) & (3 * 0) + (5 * 1)\\ (2 * 3)+ (3 * 7) & (2 * 1) + (3 * 4) & (2 * 0) + (3 * 1)\\\end{bmatrix}\\\\ &AB = \begin{bmatrix}(3)+ (7) & (1) + (4) & (0) + (1)\\ (9)+ (35) & (3) + (20) & (0) + (5)\\ (6)+ (21) & (2) + (12) & (0) + (3)\\\end{bmatrix}\\\\ &AB = \begin{bmatrix}10 & 4 & 1\\ 44 & 23 & 5\\ 27 & 14 & 3\end{bmatrix} \end{aligned}

The matrix $A$ has a size of $m \times n$ where $m = 3$ and matrix $B$ has a size of $n \times p$ where $p = 3$ . The size of resultant matrix $AB$ is $m \times p$ which is $3 \times 3$ .

Properties of Matrix Multiplication

Since, matrix operation is mathematical operations, therefore, matrix multiplication must preserve all or some of the properties with respect to multiplication operator.

Commutative Law

Suppose we multiply two matrix $A$ and $B$ ,

\begin{aligned} &A = \begin{bmatrix}2 & 2\\ 3 & 1\end{bmatrix} B = \begin{bmatrix}1 & 2\\ 5 & 2\end{bmatrix}\\\\ &AB = \begin{bmatrix}12 & 8\\ 8 & 8\end{bmatrix}\\\\ &Similarly, \\\\ &B = \begin{bmatrix}1 & 2\\ 5 & 2\end{bmatrix} A = \begin{bmatrix}2 & 2\\ 3 & 1\end{bmatrix}\\\\ &BA = AB = \begin{bmatrix}8 & 4\\ 16 & 12\end{bmatrix}\\\\ &AB \neq BA \end{aligned}

From the example above, it is clear that the product of $AB$ is not equal to the product of $BA$ . Hence, the commutative law does not work in the case of matrix multiplication.

Associative Law of Matrix Multiplication

The associative law in matrix multiplication involves more than two matrices in following ways.

Let A, B, and C be three matrices that meet the conditions of matrix multiplication.Then,

\begin{aligned} A * ( B * C ) = (A * B) * C \end{aligned}

We can test the above property with the help of an example. Let $A, B$ and $C$ be 3 square matrices of size $2 \times 2$ .

\begin{aligned} &A = \begin{bmatrix}1 & 2\\3 & 4\end{bmatrix} B = \begin{bmatrix}2 & 3\\4 & 5\end{bmatrix} C = \begin{bmatrix}3 & 2\\1 & 1\end{bmatrix}\\\\ &BC = \begin{bmatrix}9 & 7\\17 & 13\end{bmatrix}\\\\ &A * (BC) = \begin{bmatrix}43 & 33\\95 & 73\end{bmatrix}\\\\ &Similarly, \\\\ &AB = \begin{bmatrix}10 & 13\\22 & 29\end{bmatrix}\\\\ &(AB) * C = \begin{bmatrix}43 & 33\\95 & 73\end{bmatrix}\\\\ &Therefore, \\\\ &A * (B * C) = (A * B) * C \end{aligned}

The above example, both side of the equation gives same results. Thus, the associative law is true for matrix multiplication.

Identity Law

In mathematics, an identity element is a value when added element ‘a’ will give ‘a’ itself. We know that identity of addition is 0.

\begin{aligned} &a + 0 = a\\\\ &For \hspace{5px}multiplication,\\\\ &a * 1 = 1 \end{aligned}

Since, 1 is the identity element of multiplication, we need a matrix with main diagonals as 1s, such a matrix is called an identity matrix or unit matrix denoted by $I_{n}$ where $n$ is the size $n \times n$ . Therefore, identity matrix is a square matrix.

Let A be a square matrix of size 2 x 2 and I be identity matrix of size 2 x 2. Then,

\begin{aligned} &A = \begin{bmatrix}2 & 4\\4 & 6\end{bmatrix} I_{2} = \begin{bmatrix} 1 & 0\\0 & 1\end{bmatrix}\\\\ &A.I_{2} = \begin{bmatrix}2 + 0 & 0 + 4\\4 + 0 & 0 + 6\end{bmatrix}\\\\ &A.I_{2} = \begin{bmatrix}2 & 4\\4 & 6\end{bmatrix} \end{aligned}

The unit matrix when multiplied with matrix $A$ gives the same matrix $A$ as result. Therefore, identity law is true for matrix multiplication.

Commutative Property For Identity Law

We mentioned earlier that the commutative property does not apply for matrix multiplication. However, in the case of multiplying a matrix $A$ with an identity matrix $I_{n}$ , the commutative property is true.

For example, let us take previous example where we found following results.

\begin{aligned} A.I_{2} = \begin{bmatrix}2 & 4\\4 & 6\end{bmatrix} \end{aligned}

We must find $I_{n}A$ to verify our claim that the commutative law does work when multiplied with an identity matrix.

Let A be a square matrix of size 2 x 2 and I be identity matrix of size 2 x 2. Then

\begin{aligned} &I_{2} = \begin{bmatrix} 1 & 0\\0 & 1\end{bmatrix} A = \begin{bmatrix}2 & 4\\4 & 6\end{bmatrix}\\\\ &I_{2}. A = \begin{bmatrix}2 + 0 & 4 + 0\\0 + 4 & 0 + 6\end{bmatrix}\\\\ &A.I_{2} = \begin{bmatrix}2 & 4\\4 & 6\end{bmatrix} \end{aligned}

Clearly, commutative law is true in the case of matrix multiplication if one of the matrix is identity matrix. You can try to perform the multiplication with more than two matrices. Therefore, $A.I_{n} = I_{n}.A = A$ .

In the next post, we will discuss about taking transpose of a matrix.