Inverse Of Diagonal Matrix

by

The diagonal matrix has diagonal elements only and if the diagonals are 1 then the matrix is called and identity matrix I. In this article, we discuss about diagonal matrix and properties. Then find the inverse of diagonal matrix.

What is a diagonal matrix ?

A diagonal matrix is a n \times n matrix whose diagonal entries are non-zero and all other entries are zero. For example, 

A = \begin{bmatrix}a_{11}&0&0\\0&a_{22}&0\\0&0&a_{33}\end{bmatrix}

The matrix A above is a diagonal matrix whose diagonal entries are a_{11}, a_{22}, a_{33} and other entries are 0.

Some Interesting Properties of Diagonal Matrix

The diagonal matrix have some interesting properties explain in this section with examples.

Addition Or Multiplication of Diagonal Matrices

Addition or multiplication of two or more diagonal matrices of same order will give a diagonal matrix of same order.

Example #1

Let A and B be two diagonal matrices of order 3 \times 3. 

A = \begin{bmatrix}2 & 0 & 0 \\0 & 7 & 0\\0 & 0 & 4\end{bmatrix} B = \begin{bmatrix}1 & 0 & 0 \\0 & 3 & 0\\0 & 0 & 5\end{bmatrix}

Therefore, adding A and B will give C

A + B = C 

C_{3\times3} = \begin{bmatrix}2 + 1 & 0 + 0 & 0 + 0\\0 + 0 & 7 + 3& 0+0\\ 0+0& 0 + 0&4+ 5\end{bmatrix} = \begin{bmatrix}3 & 0 & 0 \\0 & 10 & 0\\0 & 0 & 9\end{bmatrix}_{3\times3}

Example #2

Let C and D be two diagonal matrices of order 2 \times 2. 

C = \begin{bmatrix}4 & 0\\0 & 3\end{bmatrix} D =\begin{bmatrix} 1 & 0\\0 & 6\end{bmatrix}

Therefore, multiplying matrix C and D will give

C \times D = F

F_{2\times2} = \begin{bmatrix}4 + 0 & 0 + 0\\0 + 0&0 + 18\end{bmatrix}= \begin{bmatrix}4 & 0\\0 & 18\end{bmatrix}_{2\times2}

Multiplication Of Diagonal Matrix With Other Matrices

Let A be matrix of order n \times n and B be a matrix of order n\times m.

Example #3

A = \begin{bmatrix}a_{11}&0&0\\0&a_{22}&0\\0&0&a_{33}\end{bmatrix}

B = \begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\\b_{31}&b_{32}\end{bmatrix}

A \times B = \begin{bmatrix}a_{11}&0&0\\0&a_{22}&0\\0&0&a_{33}\end{bmatrix} \times \begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\\b_{31}&b_{32}\end{bmatrix}

A \times B = \begin{bmatrix}a_{11}b_{11}&a_{11}b_{12}\\a_{22}b_{21}&a_{22}b_{22}\\a_{33}b_{31}&a_{33}b_{32}\end{bmatrix}

Each element of diagonal matrix A is multiplied with corresponding row elements of matrix B. For example, element a_{11} from diagonal matrix A is multiplied with all elements of first row in matrix B.

Example #4

Another case of multiplication is when matrix C of order m \times n is multiplied with a diagonal matrix A of order n \times n.

Let C be a matrix of order 4 \times 3 

C = \begin{bmatrix}c_{11}&c_{12}&c_{13}\\c_{21}&c_{22}&c_{23}\\c_{31}&c_{32}&c_{33}\\c_{41}&c_{42}&c_{43}\end{bmatrix}

and A be a diagonal matrix of order 3 \times 3

A = \begin{bmatrix}a_{11}&0&0\\0&a_{22}&0\\0&0&a_{33}\end{bmatrix}

C \times A = \begin{bmatrix}c_{11}&c_{12}&c_{13}\\c_{21}&c_{22}&c_{23}\\c_{31}&c_{32}&c_{33}\\c_{41}&c_{42}&c_{43}\end{bmatrix}\times \begin{bmatrix}a_{11}&0&0\\0&a_{22}&0\\0&0&a_{33}\end{bmatrix}

C \times A = \begin{bmatrix}c_{11}a_{11}+0+0&0+c_{12}a_{22}+0&0+0+c_{13}a_{33}\\c_{21}a_{11}+0+0&0+c_{22}a_{22}+0&0+0+c_{23}a_{33}\\c_{31}a_{11}+0+0&0+c_{32}a_{22}+0&0+0+c_{33}a_{33}\\c_{41}a_{11}+0+0&0+c_{42}a_{22}+0&0+0+c_{43}a_{33}\end{bmatrix}

C \times A = \begin{bmatrix}c_{11}a_{11}&c_{12}a_{22}&c_{13}a_{33}\\c_{21}a_{11}&c_{22}a_{22}&c_{23}a_{33}\\c_{31}a_{11}&c_{32}a_{22}&c_{33}a_{33}\\c_{41}a_{11}&0+c_{42}a_{22}&c_{43}a_{33}\end{bmatrix}

When matrix C$ is multiplied with diagonal matrix A then each element of A is multiplied with corresponding columns in matrix C. For example, element a_{11} is multiplied with first column of the matrix C.

Commutative Property of Multiplication in Between Diagonal Matrices

If two matrices A and B are diagonal matrices of same order n \times n, then the multiplication is commutative.

Example #5

Let A be a diagonal matrix of order 3 \times 3 

A = \begin{bmatrix}3&0&0\\0&4&0\\0&0&5\end{bmatrix}

and B be a diagonal matrix of order 3 \times 3

A = \begin{bmatrix}-2&0&0\\0&1&0\\0&0&7\end{bmatrix}

A \times B = \begin{bmatrix}3&0&0\\0&4&0\\0&0&5\end{bmatrix} \times \begin{bmatrix}-2&0&0\\0&1&0\\0&0&7\end{bmatrix}

A \times B = \begin{bmatrix}-6&0&0\\0&4&0\\0&0&35\end{bmatrix}

Similarly, 

B \times A = \begin{bmatrix}-2&0&0\\0&1&0\\0&0&7\end{bmatrix}\times \begin{bmatrix}3&0&0\\0&4&0\\0&0&5\end{bmatrix}

A \times B = \begin{bmatrix}-6&0&0\\0&4&0\\0&0&35\end{bmatrix}

Therefore, AB = BA for diagonal matrices is true.

Diagonal Matrix is Symmetric

If A is a diagonal matrix of order n \times n then it is symmetric.

A = A^T

Example #6

Let D be a diagonal matrix of order 4 \times 4.

A = \begin{bmatrix}a_{11}&0&0&0\\0&a_{22}&0&0\\0&0&a_{33}&0\\0&0&0&a_{44} \end{bmatrix}

When we take transpose of a matrix, then a_{ij} becomes a_{ji}, but for a diagonal matrix i = j, therefore,

A^T = \begin{bmatrix}a_{11}&0&0&0\\0&a_{22}&0&0\\0&0&a_{33}&0\\0&0&0&a_{44} \end{bmatrix} = A

A = A^T

We conclude that the diagonal matrix A is symmetric and A = A^T is true.

Power of Diagonal Matrix

If a diagonal matrix P is multiplied by itself k-times, then we can say that the matrix P is raised to the power of k.

Example #7

Let P be a diagonal matrix of order 2 \times 2. Let matrix P is raised to power k = 3 then

 P^3 = \begin{bmatrix}a & 0\\0 & b\end{bmatrix} \times \begin{bmatrix}a & 0\\0 & b\end{bmatrix}\times \begin{bmatrix}a & 0\\0 & d\end{bmatrix}

 P^3 = \begin{bmatrix}a^3 & 0\\0 & b^3\end{bmatrix}

Therefore, 

P^k = \begin{bmatrix}a^k & 0\\0 & b^k\end{bmatrix}

Invertible Diagonal Matrix

Any matrix is invertible if its determinant is not equal to 0 and it is a square matrix. The diagonal matrix is a square matrix, but it must have a non-zero entry in the main diagonal to be invertible.

If the main diagonal has a zero entry then it is a singular matrix for two reasons

  1. It is not a square matrix
  2. It has a zero determinant

Example #8

Let matrix A be a diagonal matrix of order 3 \times 3.

A = \begin{bmatrix} a & 0 & 0\\0 & b & 0\\0 & 0 & 0\end{bmatrix}

Rule 1: Diagonal matrix must be a square matrix 

The last row of matrix A is zero and must be deleted. The remaining two row is not a square matrix; therefore, not invertible.

Rule 2: The determinant of matrix A should be non-zero.

The minor matrix of A is 

= \begin{bmatrix}0 & 0 &0\\0 & 0 & 0\\0 & 0 & ab\end{bmatrix}

The determinant of a diagonal matrix A is |A| = abc + 0 + 0 = abc if there are non-zero elements in the main diagonal.

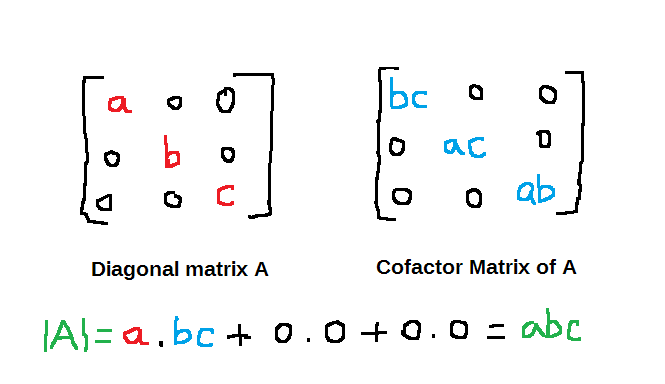
Figure 1 - Determinant of diagonal matrix A with non-zero entries in main diagonal
Figure 1 – Determinant of diagonal matrix A with non-zero entries in main diagonal

Inverse of a Diagonal Matrix

The inverse of a diagonal matrix can be found by using the following equation.

A^{-1} = \frac{\strut 1}{\strut |A|} \times adj A

Example #9

Let A be a diagonal matrix of order 3 \times 3.

A = \begin{bmatrix}a & 0 & 0\\0 & b & 0\\0 & 0 & c\end{bmatrix}

From the discussion above we know that the cofactor matrix of A is 

= \begin{bmatrix}bc & 0 & 0\\0 & ac & 0\\0 & 0 & bc\end{bmatrix}

Since, matrix A is symmetric, that is, A = A^T.

adj A = \begin{bmatrix}A_{ij}\end{bmatrix}^T = \begin{bmatrix}bc & 0 & 0\\0 & ac & 0\\0 & 0 & bc\end{bmatrix}

Therefore, 

A^{-1} = \frac{\strut 1}{\strut abc}\times \begin{bmatrix}bc & 0 & 0\\0 & ac & 0\\0 & 0 & bc\end{bmatrix}

A^{-1} = \begin{bmatrix}\frac{\strut 1}{\strut a} & 0 & 0\\0 & \frac{\strut 1}{\strut b} & 0\\0 & 0 & \frac{\strut 1}{\strut c}\end{bmatrix}

From the example it is clear that the inverse of a diagonal matrix A^{-1} contains reciprocal of each element of the diagonal matrix A.

‘Example #10

Find the inverse of following diagonal matrix B.

B = \begin{bmatrix}-3 & 0 & 0 \\0 & 2 & 0 \\ 0 & 0 & 5\end{bmatrix}

Solution :

Given the diagonal matrix B.

B = \begin{bmatrix}-3 & 0 & 0 \\0 & 2 & 0 \\ 0 & 0 & 5\end{bmatrix}

We simply need to find the inverse of each diagonal element in the matrix B.

Therefore, 

B^{-1} = \begin{bmatrix}\frac{\strut -1}{\strut 3} & 0 & 0 \\0 & \frac{\strut 1}{\strut 2} & 0 \\ 0 & 0 & \frac{\strut 1}{\strut 5}\end{bmatrix}

Important Points To Remember

Here are some important points to remember.

  • diagonal addition and multiplication with another diagonal matrix is commutative.
  • diagonal matrix is symmetric.
  • power of diagonal matrix is power of individual diagonal entries.
  • invertible diagonal matrix has non-zero diagonal entries.
  • inverse of a diagonal matrix is a matrix that has inverse of each corresponding element from the diagonal matrix.
Previous
Next