Previous article, you learned about minors of a square matrix which are determinant of smaller 2 x 2 matrix obtained by excluding row and column of a selected element from the original matrix. These minors are arranged in matrix form called matrix of minors.
However, matrix of minors is not useful in finding the adjoint as well as determinant of the original matrix. To make this point clear , let ![]() be a square matrix and its matrix of minors is
be a square matrix and its matrix of minors is ![]() which is useless unless we find cofactor matrix that assignes positive or negative signs to each minor.
which is useless unless we find cofactor matrix that assignes positive or negative signs to each minor.
The other way to look at assigning positive or negative sign is basically process of finding the odd or even class for each minor element. To know more about odd and even class read: Introduction to determinants.
How To Find Cofactor Of A Square Matrix
There are two ways to find the cofactors of a given matrix – the easy way and the hard way. Let us look at the hard way first and then move on to the easy way.
Hard Way To Find Cofactors
The steps to find the cofactor of a square matrix is
- Given a square matrix of size
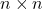 , find the matrix of minors for
, find the matrix of minors for  .
. - From the matrix of minors for
 find all cofactors using the following formula.
find all cofactors using the following formula.
Suppose ![]() , then its minor is
, then its minor is ![]() . The cofactor of
. The cofactor of ![]() is given by formula.
is given by formula.
A_{ij} = (-1)^{i + j}.M_{ij}- Arrange all the cofactors in matrix form according to their subscript value.
Example #1
Find the cofactors of square matrix ![]() of order
of order ![]() .
.
A = \begin{bmatrix}2 &5 & 1\\1 & 3 & 7\\4 & 2 & 6\end{bmatrix}Solution:
Given the matrix ![]() of order
of order ![]() , let us find all the minors.
, let us find all the minors.
A = \begin{bmatrix}2 &5 & 1\\1 & 3 & 7\\4 & 2 & 6\end{bmatrix}Minors are as follows.
\begin{aligned}
&M_{11} = 18 - 14 = 4\\\\
&M_{12} = 6 - 28 = -22\\\\
&M_{13} = 2 - 12 = -10\\\\
&M_{21} = 30 - 2 = 28\\\\
&M_{22} = 12 - 4 = 8&\\\\
&M_{23} = 4 - 20 = -16\\\\
&M_{31} = 35 - 3 = 32\\\\
&M_{32} = 14 - 1 = 13\\\\
&M_{33} = 6 - 5 = 1
\end{aligned}We can arrange the minor in matrix form,
= \begin{bmatrix}4 & -22 & -10\\28 & 8 & -1\\32 & 12 & 1\end{bmatrix}Compute the cofactors from minors,
\begin{aligned}
&A_{11} = (-1)^{1+1}.M_{11} = (1)(4)= 4\\\\
&A_{12} = (-1)^{1+2}.M_{12} = (-1)(-22)= 22\\\\
&A_{13} = (-1)^{1+3}.M_{13} = (1)(-10)= -10\\\\
&A_{21} = (-1)^{2+1}.M_{21} = (-1)(28)= -28\\\\
&A_{22} = (-1)^{2+2}.M_{22} = (1)(8)= 8\\\\
&A_{23} = (-1)^{2+3}.M_{23} = (-1)(-16)= 16\\\\
&A_{31} = (-1)^{3+1}.M_{31} = (1)(32)= 32\\\\
&A_{32} = (-1)^{3+2}.M_{32} = (-1)(13)= -13\\\\
&A_{33} = (-1)^{3+3}.M_{33} = (1)(1)= 1
\end{aligned}The matrix of cofactors is,
\begin{bmatrix}4 & 22 & -10\\-28 & 8 & 16\\32 & -13 & 1\end{bmatrix}Easy Way To Find Cofactors
The easy way to find cofactor is to simply assign + or – based on the position of the minors in the matrix of minors. Each position is known to have a sign depending on ![]() and
and ![]() value.
value.
= \begin{bmatrix}+ & - & +\\- & + & -\\+ & - & +\end{bmatrix}Next use the sign matrix as reference change the sign for each minor.
= \begin{bmatrix}4 & -22 & -10\\28 & 8 & -1\\32 & 12 & 1\end{bmatrix}will be,
= \begin{bmatrix}(+)4 & (-)-22 & (+)-10\\(-)28 & (+)8 & (-)-16\\(+)32 & (-)12 & (+)1\end{bmatrix}and finally gives you cofactor matrix.
=\begin{bmatrix}4 & 22 & -10\\-28 & 8 & 16\\32 & -12 & 1\end{bmatrix}Finding The Determinant Of Matrix Using Cofactor
Finding the determinant of a matrix is easy when you have the cofactor matrix. There are only 3 steps.
- Pick a row or a column from original matrix

- Pick the corresponding row or column from cofactor matrix of

- Multiply corresponding terms and add them together to get the single determinant value.
Example #2
Find the determinant of the following matrix ![]() whose cofactor matrix is given.
whose cofactor matrix is given.
\begin{aligned}
&A = \begin{bmatrix}2 &5 & 1\\1 & 3 & 7\\4 & 2 & 6\end{bmatrix}\\\\
&\begin{bmatrix}A_{ij}\end{bmatrix} =\begin{bmatrix}4 & 22 & -10\\-28 & 8 & 16\\32 & -12 & 1\end{bmatrix}
\end{aligned}Solution:
\begin{aligned}
&A = \begin{bmatrix}2 &5 & 1\\1 & 3 & 7\\4 & 2 & 6\end{bmatrix}\\\\
&\begin{bmatrix}A_{ij}\end{bmatrix} =\begin{bmatrix}4 & 22 & -10\\-28 & 8 & 16\\32 & -12 & 1\end{bmatrix}
\end{aligned}Let us choose row 1 from both matrix A and cofactor matrix and multiply each corresponding element.
\begin{aligned}
&= 2(4) + 5(22) + 1(-10)\\\\
&= 8 + 110 - 10 \\\\
&|A| = 108
\end{aligned}Let us see another example, we choose column 2 and corresponding column 2 from cofactor matrix. Multiply each corresponding elements.
\begin{aligned}
&= 5(22) + 8 (3) 2(-13)\\\\
&= 110 + 24 - 26\\\\
&|A| = 108
\end{aligned}We encourage you to try some more examples to understand the method completely. In the next, we will discuss about deriving adjoint of a matrix for finding inverse of a matrix.