In the previous article, you have learned simple way of cross multiplication to obtain the determinant of a square matrix. As the size of matrix get larger and larger it is increasing difficult to compute the determinant because we must first select an element and then extract smaller matrix from the larger matrix and find the determinant of the smaller matrix.
The smaller matrix that corresponds to an element of the original matrix is called its Minor.
The Matrix Of Minor
Though minor of a matrix is helpful in finding the determinant of a larger matrix, the main purpose is to find an adjugate matrix or adjoint matrix. Finding minors of all the elements of the matrix is the first step towards finding adjoint matrix.
The matrix made of all minor is called a matrix of minors.
The minor of a matrix is denoted as ![]() is nothing but a determinant of a smaller matrix obtained from original larger matrix.
is nothing but a determinant of a smaller matrix obtained from original larger matrix.
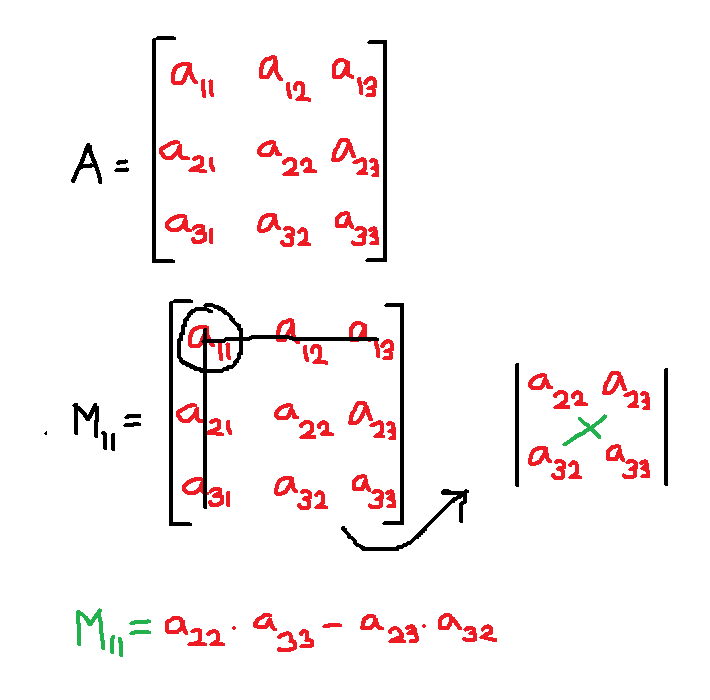
To find the minor you must follow these steps:
Step 1: Select an element to find its minor from the original matrix, for instance, ![]() .
.
In the above matrix ![]() we have selected element
we have selected element ![]() and its minor is
and its minor is ![]() .
.
Step 2: The next step is to cross out corresponding row and column that has element ![]() .
.
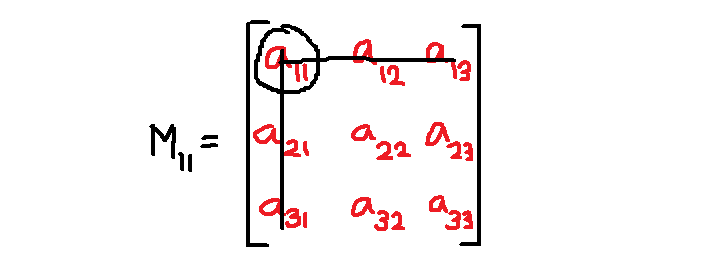
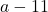
The element ![]() is in row
is in row ![]() and column
and column ![]() ; therefore, cross out row
; therefore, cross out row ![]() and column
and column ![]() .
.
Step 3: Find the determinant of the smaller matrix obtained after step 2.
After step 2, we can use the remaining smaller matrix and do a cross multiplication to find the determinant. The determinant so obtained is the minor ![]() . There will be 9 minors for 9 elements of matrix A.
. There will be 9 minors for 9 elements of matrix A.
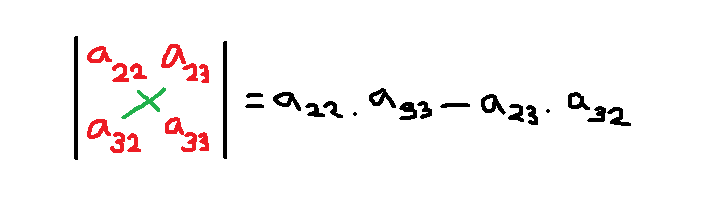
Construct Matrix of Minors
Once we have obtained minors all element of the matrix ![]() , arrange them as a matrix called matrix of minors.
, arrange them as a matrix called matrix of minors.
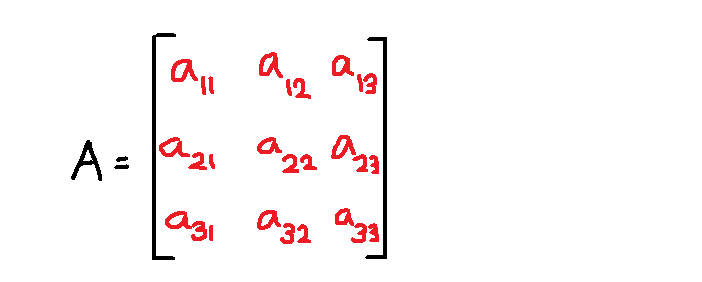
Here we compute the matrix of minors from original matrix ![]() .
.
\begin{aligned}
&M_{11} = a_{22}.a_{33} - a_{23}.a_{32}= c_{11}\\
&M_{12} = a_{21}.a_{33} - a_{23}.a_{31}= c_{12}\\
&M_{13} = a_{21}.a_{32} - a_{22}.a_{31}= c_{13}\\\\
&M_{21} = a_{12}.a_{33} - a_{13}.a_{32}= c_{21}\\
&M_{22} = a_{11}.a_{33} - a_{13}.a_{31}= c_{22}\\
&M_{23} = a_{11}.a_{32} - a_{12}.a_{31}= c_{23}\\\\
&M_{31} = a_{12}.a_{23} - a_{13}.a_{22}=c_{31}\\
&M_{32} = a_{11}.a_{23} - a_{13}.a_{21}=c_{32}\\
&M_{33} = a_{11}.a_{22} - a_{12}.a_{21}=c_{33}\\\\
&= \begin{bmatrix}c_{11} & c_{12} & c_{13}\\c_{21} & c_{22} & c_{23}\\c_{31} & c_{32}& c_{33}\end{bmatrix}
\end{aligned}A Few Examples
Q1: Find the minor for matrix ![]() and write the matrix of minors.
and write the matrix of minors.
A= \begin{bmatrix}2 & -1\\4 & 5\end{bmatrix}Solution:
Given the following 2 x 2 matrix.
A= \begin{bmatrix}2 & -1\\4 & 5\end{bmatrix}If we select any element in matrix A and cross out the row and column corresponding there is only one element remains. But, remember that a single element is 1 x 1 square matrix and we have to find determinant of that single element.
\begin{aligned}
&M_{11} = |5| = 5\\
&M_{12} = |4| = 4\\
&M_{21} = |-1| = -1\\
&M_{22} = |2| = 2
\end{aligned}The matrix of minors is,
= \begin{bmatrix}5 & 4\\-1 & 2\end{bmatrix}Q2: Find the minors for the following ![]() matrix.
matrix.
A = \begin{bmatrix}2 & 1 & 3\\-3 & 5 & 1\\6 &2 & -5\end{bmatrix}Solution:
The Minors are,
\begin{aligned}
&M_{11} = 5 . -5 - 1 . 2 = -25 - 2 = -27\\
&M_{12} = -3 . -5 - 1 . 6 = 15 - 6 = 9\\
&M_{13} = -3 . 2 - 5 . 6 = -6 - 30 = -36\\\\
&M_{21} = 1 . -5 - 3 . 2 = -5 - 6 = -11\\
&M_{22} = 2 . -5 - 3 . 6 = -10 - 18 = -28\\
&M_{23} = 2 . 2 - 1 . 6 = 4 - 6 = -2\\\\
&M_{31} = 1 . 1 - 5 . 3 = 1 - 15 = -14\\
&M_{32} = 2 . 1 - (3) . (-3) = 2 + 9 = 11\\
&M_{33} = 2 . 5 - 1 . (-3) = 10 + 3 = 13
\end{aligned}The matrix of minors is,
= \begin{bmatrix}-27 & 9 & -36\\-11 & -28 & -2\\-14 & 9 & 13\end{bmatrix}The minor so found is useful in finding cofactors and adjoint of a given square matrix. We shall also see that minor are useful tool in solving a system of linear equations by determinant method in future articles.