Introduction To Exponential Functions

Table of Contents

In this post, I am going to introduce you to the concept of exponential functions. A function that use exponents is the exponential function and it has many uses while calculating growth. You can determine, how fast something is growing with these kinds of functions. When it comes to calculating growth of something like population, for animals, or anything, exponential functions are much faster than any other functions. Therefore, it becomes an important topic of study.

Think of a certain kind of cell that doubles everyday. How do you represent this as a function ? Let’s create a table of values and see how the cell grows within 5 days.

Advertisements

Day	Number of Cells (doubles everyday)
1	1
2	2
3	4
4	8
5	16

Table 1 – Growth of Cells in 5 days

Now, you see that this growth can be represented as power of 2 because each of the cells double next day.

Given any day I must be able to compute the number of cells for that day. On day $1$ , the growth is $2^0 = 1$ . Here, the exponent is $0$ that because we have no growth on first day.

For any day, you can calculate the number of cells using function $f(x-1) = 2^{x-1}$ where $x$ represent the particular day on which you want to know the number of cells count.

On day 5, we have $f(5) = 2^{5-1} = 2^4 = 16$ cells. Can you imagine how fast this grows ?

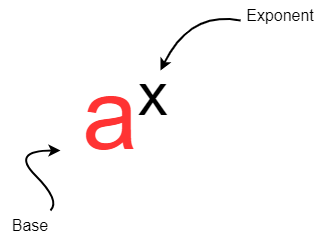
Any exponential function has base and an exponent and keeping this in mind, let me define the exponential function.

Definition Of Exponential Functions

Any function $f(x)$ with base $b$ is defined as

\begin{aligned} &f(x) = b^x \\ \\ &or \\ \\ &y = b^x \end{aligned}

What is not exponential functions?

Consider the following functions.

\begin{aligned} &f(x) = (-3)^x \\ \\ &f(x) = 1^{x+1}\\ \\ &f(x) = x^x \\\\ &f(x) = x^2 \end{aligned}

You have to remember two rules for exponential functions, (1) base is a positive constant greater than $0$ and not equal to $1$ (2) exponent is a variable representing real number. The functions above violates one or both rules, hence, they are not exponential functions.

The function $f(x) = (-3)^x$ will give negative results for odd values of $x$ and positive results for even values of $x$ .

For example, $f(2) = (-3)^2 = 9$ , but $f(3) = (-3)^3 = -27$ . Therefore, it is not an exponential function.

The next function above, $f(x) = 1^{x +1}$ has proper structure, except that it violates the rule 1, $b \neq 1$ .

Similarly, the function $f(x) = x^2$ and $f(x) = x^x$ violates rule 1 which says base must be a positive constant, not variable. Also, exponent cannot be a constant which is the violation of rule 2.

Definition Of Exponential Functions

What is not exponential functions?

Graph Of Exponential Functions

Ads Blocker Detected!!!