The transpose of a matrix is denoted by ![]() is obtained by changing rows into columns or columns to rows of a matrix
is obtained by changing rows into columns or columns to rows of a matrix ![]() . If size of the matrix
. If size of the matrix ![]() is
is ![]() then the size of the transposed matrix
then the size of the transposed matrix ![]() is
is ![]() .
.
Transpose Of A Matrix
The element in ![]() row and
row and ![]() column of matrix
column of matrix ![]() becomes the
becomes the ![]() row and
row and ![]() column element in matrix
column element in matrix ![]() .
.
\begin{aligned}
&(A^T)_{ij} = (A)_{ji}
\end{aligned}Let ![]() be a matrix of size
be a matrix of size ![]() .
.
\begin{aligned}
A = \begin{bmatrix}a & b\\ c & d\\ e & f\end{bmatrix}
\end{aligned}Transpose of matrix ![]() .
.
\begin{aligned}
A^T = \begin{bmatrix}a & c & e\\ b & d & f\end{bmatrix}
\end{aligned}Let us take element ‘c’ which is at 2nd row and 1st column of matrix ![]() ; after transpose operation on matrix
; after transpose operation on matrix ![]() , it is at the position of 1st row and 2nd column of matrix
, it is at the position of 1st row and 2nd column of matrix ![]() .
.
Similarly, the element ‘b’ is at the position of first row and second column of matrix ![]() , but after the transpose operation, its position changes to 2nd row and 1st column in matrix
, but after the transpose operation, its position changes to 2nd row and 1st column in matrix ![]() .
.
Example #1
Transpose the following matrix A.
\begin{aligned}
A = \begin{bmatrix}3 & 1 & 5\\ 2 & 6 & 9\end{bmatrix}
\end{aligned}The transpose of matrix ![]() is
is
\begin{aligned}
A^T = \begin{bmatrix}3 & 2\\ 1 & 6\\5 & 9\end{bmatrix}
\end{aligned}Example #2
Transpose the following matrix B.
\begin{aligned}
&A = \begin{bmatrix}1 & 5\\ 7 & 6\\8 & 4\end{bmatrix}
\end{aligned}The transpose of matrix ![]() is
is
\begin{aligned}
A^T = \begin{bmatrix}1 & 7 & 8\\ 5 & 6 & 4\end{bmatrix}
\end{aligned}Symmetric Matrix
When the transpose of the matrix is the original matrix itself, then it is called a Symmetric matrix. Suppose ![]() is a matrix of size
is a matrix of size ![]() , then the transpose of matrix
, then the transpose of matrix ![]() .
.
All the elements above the diagonal is a mirror image of elements below the diagonal elements. That is, ![]() is symmetric matrix if
is symmetric matrix if ![]() for all i and j.
for all i and j.
\begin{aligned}
A = \begin{bmatrix}a_{11} & p & q\\p & a_{22} & r\\q & r & a_{33}\end{bmatrix}
\end{aligned}The elements of ![]() . The transpose of such a matrix is,
. The transpose of such a matrix is,
\begin{aligned}
A^T = \begin{bmatrix}a_{11} & p & q\\p & a_{22} & r\\q & r & a_{33}\end{bmatrix}
\end{aligned}Therefore,
\begin{aligned}
A = A^T
\end{aligned}What Are The Properties Of A Transpose Of A Matrix ?
In this section, we shall discuss about the properties of a transpose of a matrix. There are 4 interesting properties of a transpose as listed below.
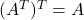 , where
, where  is a matrix of size
is a matrix of size 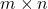 or
or 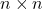 .
.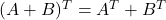 , where
, where  and
and 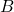 are of same size, that is,
are of same size, that is, 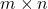 or
or 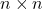 .
.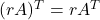 , where
, where  is matrix of size
is matrix of size 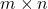 or
or 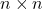 and
and  is a real number.
is a real number.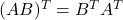 , where
, where  and
and 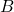 are matrices of size
are matrices of size 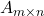 and
and 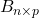 .
.
Let us verify each of the statement.
#1 : 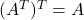
The transpose of a transpose of matrix ![]() is the original matrix
is the original matrix ![]() .
.
\begin{aligned}
Let \hspace{5px}A = \begin{bmatrix}2 & 3\\-1 & 5\end{bmatrix}
\end{aligned}Transpose of matrix ![]() .
.
\begin{aligned}
A^T = \begin{bmatrix}2 & -1\\3 & 5\end{bmatrix}
\end{aligned}Transpose of ![]() .
.
\begin{aligned}
(A^T)^T = \begin{bmatrix}2 & 3\\-1 & 5\end{bmatrix}
\end{aligned}From the results above, it is clear that ![]() where
where ![]() is a matrix of size
is a matrix of size ![]() or
or ![]() .
.
#2 : 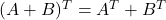
The transpose of sum of two matrices ![]() and
and ![]() of same size
of same size ![]() or
or ![]() is equal to sum of transpose of matrices
is equal to sum of transpose of matrices ![]() and
and ![]() .
.
Let ![]() and
and ![]() be two matrices of same size. Then
be two matrices of same size. Then
\begin{aligned}
&A = \begin{bmatrix}1 & 5\\-2 & 3\end{bmatrix} B = \begin{bmatrix}2 & 1\\5 & -1\end{bmatrix}\\\\
&(A + B) = \begin{bmatrix}3 & 6\\3 & 2\end{bmatrix}
\end{aligned}Transpose of matrix ![]() .
.
\begin{aligned}
(A + B)^T = \begin{bmatrix}3 & 3\\6 & 2\end{bmatrix}
\end{aligned}Now, we shall take transpose of matrix ![]() and matrix
and matrix ![]() and add them together to obtain
and add them together to obtain ![]() .
.
\begin{aligned}
A = \begin{bmatrix}1 & 5\\-2 & 3\end{bmatrix} B = \begin{bmatrix}2 & 1\\5 & -1\end{bmatrix}
\end{aligned}Transpose of A.
\begin{aligned}
A^T = \begin{bmatrix}1 & -2\\5 & 3\end{bmatrix}
\end{aligned}Transpose of B.
\begin{aligned}
B^T = \begin{bmatrix}2 & 5\\1 & -1\end{bmatrix}
\end{aligned}Sum of ![]() and
and ![]() .
.
\begin{aligned}
A^T + B^T = \begin{bmatrix}3 & 3\\6 & 2\end{bmatrix}
\end{aligned}#3 : 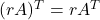
A transpose of the product of matrix ![]() with scalar
with scalar ![]() is equal to the product of scalar
is equal to the product of scalar ![]() and transpose of matrix
and transpose of matrix ![]() where size of the matrix
where size of the matrix ![]() is
is ![]() or
or ![]() and
and ![]() is a real number.
is a real number.
\begin{aligned}
&Let \hspace{5px} A = \begin{bmatrix}2 & 3\\1 & 7\end{bmatrix} \hspace{4px} and \hspace{5px} r = 2\\\\
&(rA) = \begin{bmatrix}4 & 6\\2 & 14\end{bmatrix}
\end{aligned}Transpose of ![]() ,
,
\begin{aligned}
(rA)^T = \begin{bmatrix}4 & 2\\6 & 14\end{bmatrix}
\end{aligned}Similarly, let us take transpose of ![]() .
.
\begin{aligned}
A^T = \begin{bmatrix}2 & 1\\3 & 7\end{bmatrix}
\end{aligned}The product ![]() is,
is,
\begin{aligned}
rA^T = \begin{bmatrix}4 & 2\\6 & 14\end{bmatrix}
\end{aligned}Therefore, ![]() .
.
The output of both the products are equal and the property ![]() is true for all matrices.
is true for all matrices.
#4 : 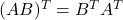
The transpose of product of two defined ( ![]() and
and ![]() ) matrices
) matrices ![]() and
and ![]() is equal to the product of transpose of matrix
is equal to the product of transpose of matrix ![]() and transpose of matrix
and transpose of matrix ![]() . Let us verify this claim with the help of an example.
. Let us verify this claim with the help of an example.
\begin{aligned}
&Let \hspace{5px}A = \begin{bmatrix}1 & 5\\2 & 1\end{bmatrix} \hspace{5px} and \hspace{5px} B = \begin{bmatrix}3 & -1\\2 & 3\end{bmatrix}\\\\
&AB = \begin{bmatrix}3 + 10 & -1 + 15\\6 + 2 & -2 + 3\end{bmatrix}= \begin{bmatrix}13 & 14\\8 & 1\end{bmatrix}
\end{aligned}Transpose of ![]() .
.
\begin{aligned}
(AB)^T = \begin{bmatrix}13 & 8\\14 & 1\end{bmatrix}
\end{aligned}Similarly, the transpose of matrix ![]() and matrix
and matrix ![]() is,
is,
\begin{aligned}
&B^T = \begin{bmatrix}3 & 2\\-1 & 3\end{bmatrix} \hspace{5px} and \hspace{5px} A^T = \begin{bmatrix}1 & 2\\5 & 1\end{bmatrix}\\\\
&B^TA^T = \begin{bmatrix}3 + 10 & 6 + 2\\-1 + 15 & -2 + 3\end{bmatrix}\\\\
&B^TA^T = \begin{bmatrix}13 & 8\\14 & 1\end{bmatrix}\\\\
&Therefore, \hspace{5px}(AB)^T = B^TA^T
\end{aligned}Once again, the product of both sides of the equation of the property ![]() holds true. The property is valid.
holds true. The property is valid.
In the next, post we will discuss more about symmetric and skew-symmetric matrices.