System of Linear Equations

May 12, 2023December 19, 2020 by admin

Table of Contents

Before you we try to understand the system of linear equations, we must understand the basic terminologies that we are going to use in the linear algebra.

Advertisements

Linear Equations

Linear equation represents a straight line on a xy-plane or co-ordinate plane.

a_{1}x + a_{2}y = b

The 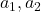$a_{1}, a_{2}$ are real number constants and both cannot be zero at the same time.
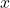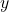The $x$ and $y$ are called variables. Hence, the equation is linear equation in variable 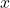$x$ and $y$ .

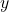Therefore, linear equation in n variable is given as

a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} + \dots + a_{n}x_{n} = b

where $a_{1}, a_{2}, a_{3} \hspace{1ex}$ and $\hspace{1ex} b$ are real number constants.

Examples of linear equations

Here are some examples of linear equations.

\begin{aligned} 3x + 5 = 13\\ \\ \frac{3}{4}y + 3z = 1 \end{aligned}

From the above examples, note that linear equations show following characteristics.

There is not term in the equation with root or product.
All variables are in power of 1.
They do not appear as an argument of another function.

Here are examples of non-linear equations to help you understand the basic differences.

\begin{aligned} &2 + \sqrt{y} = 7\\ &x + 2yz + z = 6\\ &sin \hspace{3px} x + cos \hspace{3px}x = 1 \end{aligned}

Solution Of Linear Equations

A linear equation

a_{1}x_{1} + a_{2}x_{2} + ... + a_{n}x_{n}

has a sequence of $n$ numbers

c_{1},c_{2},..., c_{n}

as solution which satisfy the equation once we substitute them with the variables.

For example,

a_{1}x_{1} + a_{2}x_{2} + a_{2}x_{2} + ... + a_{n}x_{n]} = b\\ \\

The solution is $c_{1}, c_{2},\cdots,c_{n}$
Then,
$a_{1}c_{1} + a_{2}c_{2} + a_{2}c_{2} + \cdots + a_{n}c_{n} = b$ will satisfy the equation.

The set of all solutions of a linear equation is called solution set or general solution to the linear equation.

How to find solution to linear equations ?

Now we will solve two linear equation using substitute method.

Problem #1 : solve $x + 2y = 4$ .

Solution:

We can solve like ordinary algebraic equation. Solve for x for solve for y.

Advertisements

Add $-2y$ to both side of the equation

x + 2y - 2y = 4 - 2y

now we have

x = 4 - 2y

Let’s give an arbitrary value to y. This way we get value for $x$ .

\begin{aligned} &y = 1\\ &x = 4 - 2y\\ &x = 4 - 2\\ &Therefore, \hspace{2mm}x = 2 \end{aligned}

Problem #2 : solve $x_{1} + 3x_{2} - 5x_{3} = 10$
——————————————————————————-

Solution:
————–
This time we can solve for two variables and get the third. We get following equations.

$x_{1} = 10 - 3x_{2} + 5x_{3}$

Let us give arbitrary value to $x_{2}$ and $x_{3}$ .

$x_{1} = 10 - 2(1) + 5(2)$

$x_{1} = 10 - 2 + 10$

$x_{1} = 18$

System of Linear Equations

The system of linear equations is a set of linear equations with $n$ variables $x_{1}, x_{2},x_{3}, \cdots,x_{n}$ .

\begin{aligned} &x_{1} + 5x_{2} + 2x_{3} = 6\\ &3x_{1} + x_{2} - x_{3} = 4\\ &4x_{1} + 2x_{2} + 2x_{3} = 6 \end{aligned}

The solution set $c_{1}, c_{2}, c_{3}, \cdots, c_{n}$ when replaced with variables $x_{1}, x_{2},x_{3}, \cdots, x_{n}$

will satisfy every equation in the linear system. In the above system of linear equations,

$x_{1} = 1, x_{2} = 1$ and $x_{3}= 0$

will satisfy all the equations.

In the next post, we will discuss about inconsistent and consistent system of linear equations.

Advertisements

Ads Blocker Detected!!!

We have detected that you are using extensions to block ads. Please support us by disabling these ads blocker.