Queue is a linear data structure and an abstract data type which is defined using some basic data type in programming languages. A queue data structure is implemented using an array or a linked-list type in a programming language.
There are two pointers that mark both ends of a queue.
- Front
- Rear
A queue works on FIFO principle, First In, First out, any element that goes first must come out first.
There are 3 operations performed on a queue
- Enqueue – insert element at the rear of the queue.
- Dequeue – remove elements from the front of the queue.
- Display – display elements of queue.
Enqueue Operation
The enqueue operation is performed in rear end of the queue. You cannot insert into queue data structure if queue is full. When the queue has space, the enqueue operation insert an element and update the ‘rear’ pointer by incrementing it.
For example
The current status of a queue is given below.
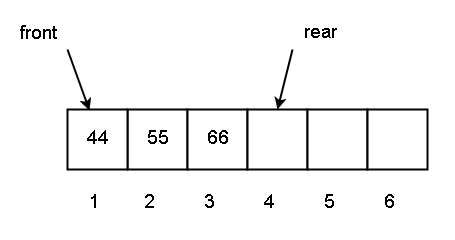
Q [1] = 44 and front = 1, Q [3] = 66 and rear = 4
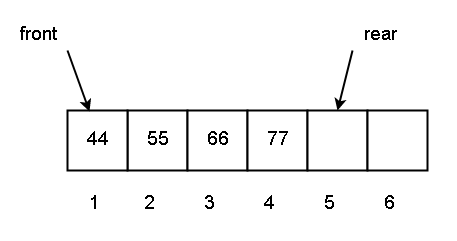
We will insert element 77 at the rear end of the queue, i.e., Q [4] = 77.
new status of the queue after enqueue operation will be following.
Dequeue Operation
Dequeue operation removes an element from the front of the queue. But the queue must not be empty for dequeue operation to work. An element from the front is removed and ‘front’ pointer is updated.
For example
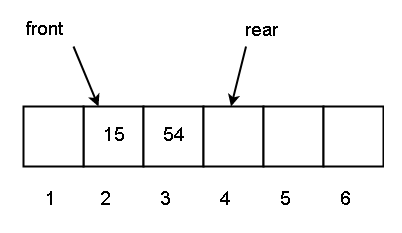
Consider the status of a queue given below
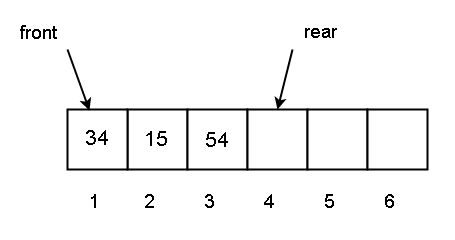
Q [1] = 34 and front = 1
You decided to delete Q [1], after deletion front = 1 + 1 = 2
The current queue is shown in following diagram,
Display Operation
This is a simple operation where we traverse through the entire queue and display the list of elements. This function is the same for both array and linked-list implementation of a queue data structure.
Types of Queues
There are different types of queues data structure about which we will learn in future lessons. The list of queues is given below.
- Circular Queue – where there is not end to the queue and elements are added or deleted in circular motion.
- Priority Queue – elements of queue are in a specific order.
- Double-Ended Queue – queue elements can be deleted or inserted from both ends.
Queue Empty and Queue full Scenario
Before inserting or deleting from queue we must check for two conditions
- Is the queue empty?
- Is the queue full?
Let’s see each scenario in more detail.
Queue Empty Scenario
When queue is initiated both front = rear = 1, but after that when front==rear then it means that the queue is empty and we cannot delete from the queue because that will be an underflow.
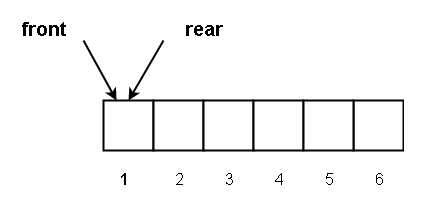
For example
Consider an array based empty queue, where front = rear = 1.
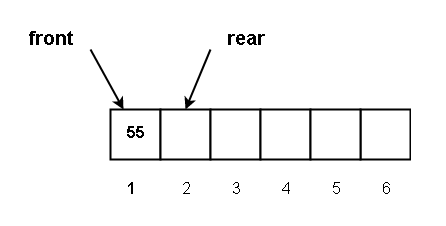
We inserted 55
Q [1] = 55, rear = 1 + 1 = 2, front = 1
This is shown in the following diagram.
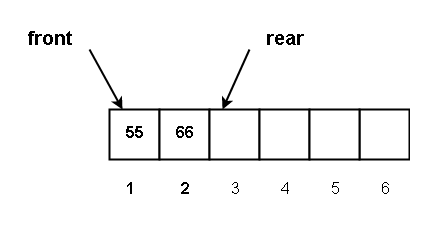
We inserted another element 66, now the queue is
Q [2] = 66, rear = 2 + 1 = 3, front = 1
Now, let’s start deleting all the elements. Delete the first element 55. Then the queue status is as follows.
Rear = 3, front = 1 + 1 = 2 and Q [2] = 66
The element Q [1] = 55 is deleted.
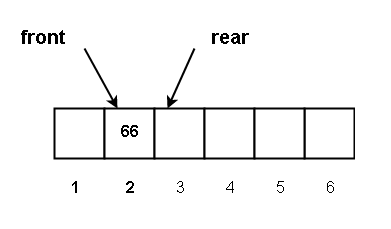
Next, we delete the element Q [2] = 66. The status of the queue after deletion is shown below.
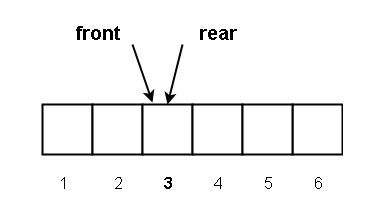
Now, front = 2 + 1 = 3, rear = 3 and since,
Front == rear
The queue is empty.
Queue Full Scenario
To insert into a queue, you need to check if the queue is full, so when the front == rear + 1, then the queue is full. Any attempt to insert a new element will result in queue overflow.
For example,
Current status of a queue is as follows
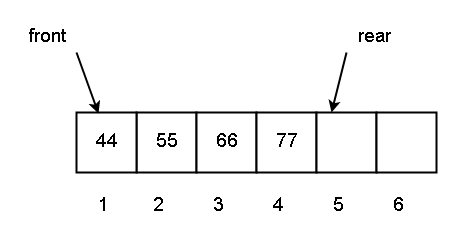
In the diagram above,
Q [1] = 44 and front = 1. Also Q [4] = 77 and rear = 5
Now we want to insert a new element 88 at Q [5].
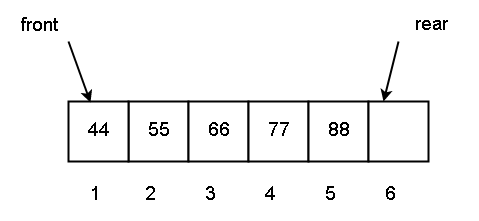
The new status of the queue will be
Q [1] = 44 and front = 1, Q [5] = 88 and rear + 1 = 5 + 1 = 6
This is shown in the queue data structure diagram below.
Now finally, you will insert at Q [6] = 99. The status of the queue becomes
Q [1] = 44 and front = 1, Q [6] = 99 and rear + 1 = 6 + 1 = 7.
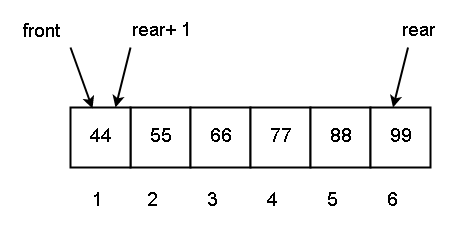
The rear value is greater than queue length. Then
rear + 1 = 7 mod 6 = 1
But,
front = rear + 1 = 1
Then the queue is full and we cannot insert more elements.
References
A.A.Puntambekar. 2009. Data Structures And Algorithms. Technical Publications.
E.Balaguruswamy. 2013. Data Structures Using C. McGraw Hill Education.
Thomas H. Cormen, Charles E. Leiserson, Ronald Rivest, Clifford Stein. 2009. Introduction to Algorithms. MIT Press.
